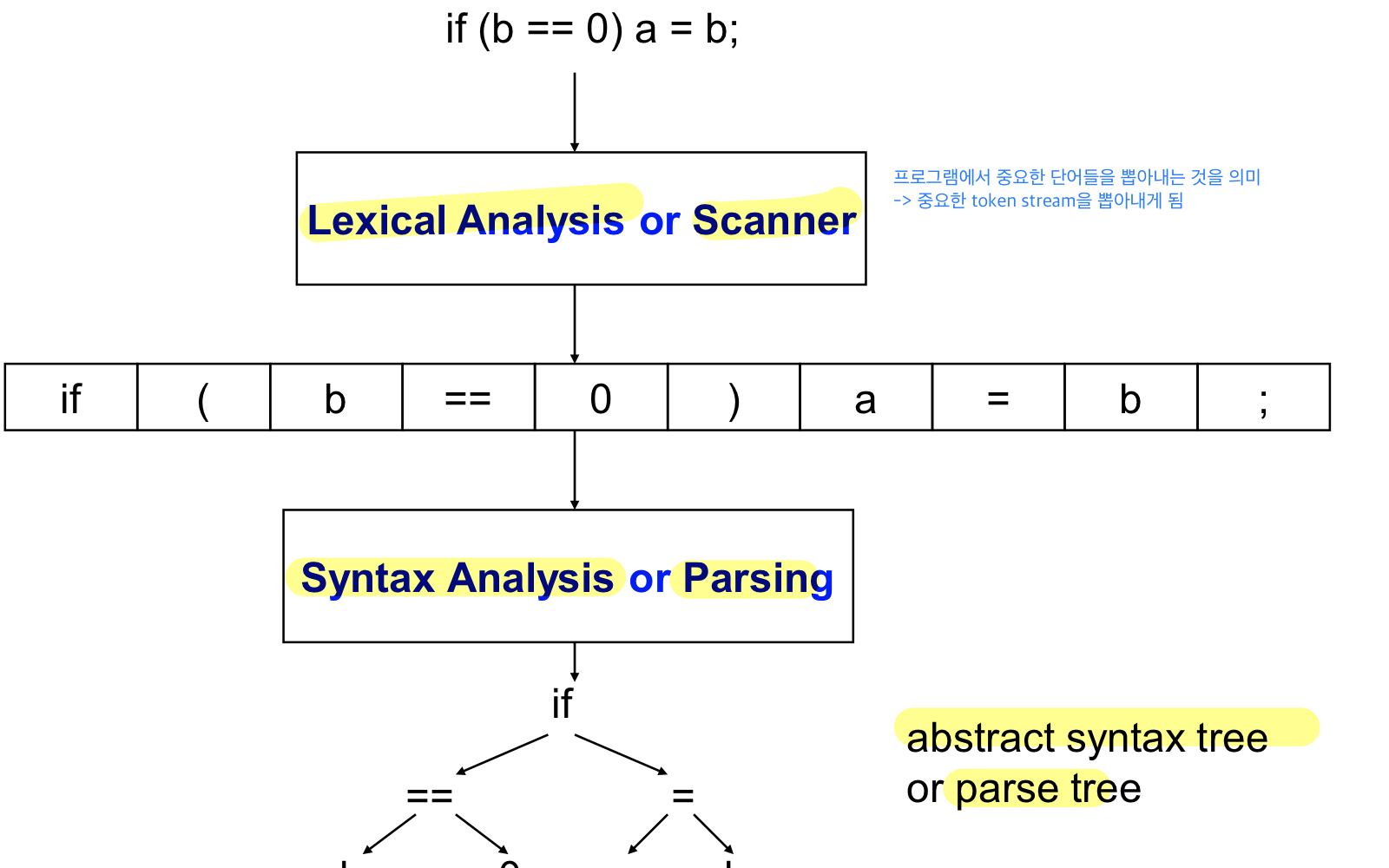
lexical analysis까지 배웠고 얘는 프로그램에서 중요한 단어들을 뽑아내는 것을 의미-> 중요한 토큰들을 뽑아내게 됨 : token stream

이걸로 syntax analysis를 수행하게 되면 토큰들이 문법에 맞도록 stream이 이루어져있는지 검사하고 문법에 맞춰서 parse tree를 만들어주게 된다(abstract syntax tree)

토큰들과의 관계를 찾는 것이며 문제가 없다면 syntax tree가 되고 나중에 어셈블리 형태로 저장된다. 이게 프론트앤드에서 가장 중요한 작업

Parsing analogy

파싱은 언어를 분석하는 것과 같다고 본다

syntax analysis for natrural languages

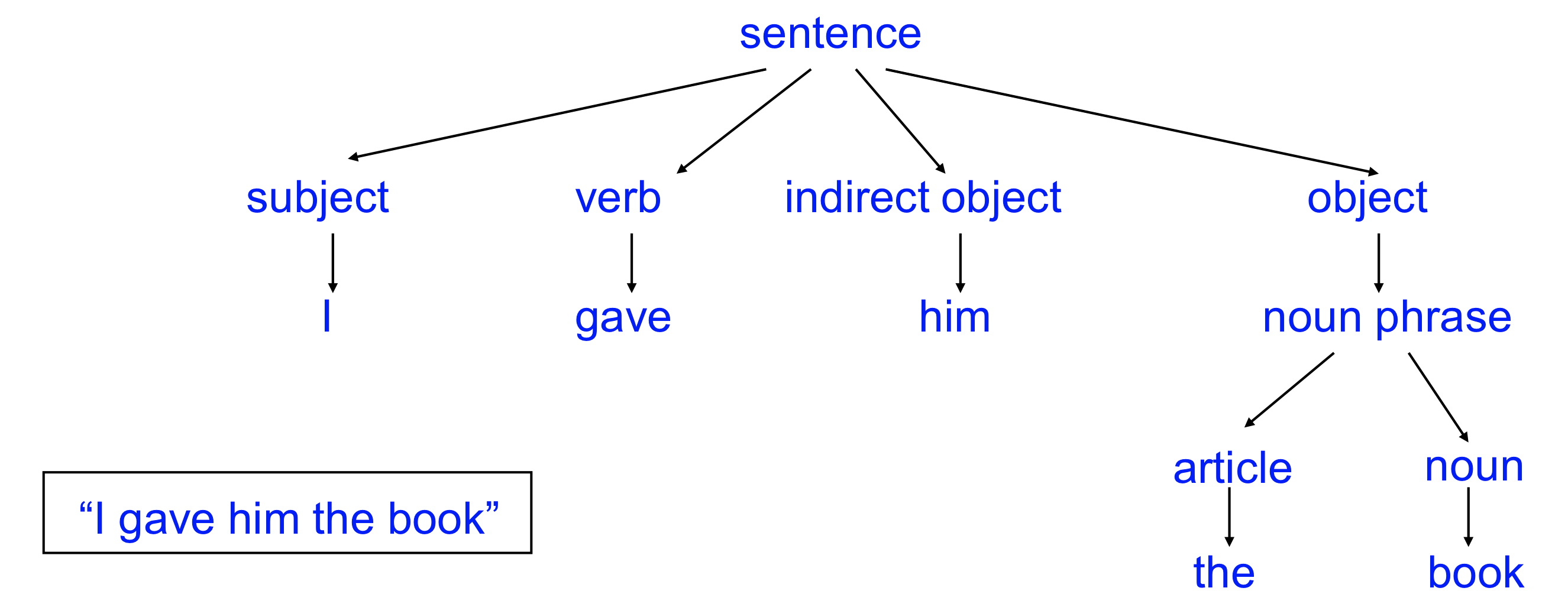
• sentence가 문법적으로 올바른지 recognize
  • 언어적인 면에서 생각해보자면 문장이 문법적으로 맞는지 확인 후 각각의 토큰(워드)의 역할을 알게 된다
• function of each word를 identify
  • 각각의 위치가 있고 법칙에 따라서 맞는 단어들이 들어가 있는지 체크
  • 문장의 토큰들을 배열한 후 각각의 토큰들의 역할을 지정하게 해주는 것이 실제 언어의 문법적인 분석

→ 컴파일러 역시 토큰 stream을 문법적으로 맞는지 확인하고 각각의 토큰들의 역할과 관계를 지정

목표

• input token stream이 있을 때 프로그램의 문법(syntax)을 만족하는지 분석하는 것을 판단하는 것을 말함

필요한 것?

• 문법(syntax)을 표현할 수 있는 방법이 필요(spec처럼) → CFG(recursion을 표현하기 위함)
• Input token stream이 지정해준 syntax spec과 맞는지 메커니즘이 필요→ LL, LR, LALR 등등…

Lexical analysis와 비교하자면 detect하는 token을 표현하기 위해서 RE를 사용했고 input stream에서 token stream을 만들기 위해서는 FA(finite automata)를 사용

RE를 그냥 사용하면 안되는 이유

RE가 있으면 DFA를 만들면 되지만 문법체크에는 능력이 부족함

• 너무 간단한 문법체크는 가능하지만 재귀적인 부분(unbound counting)을 해결할 수 없다
• 가장 많이 문제가 되는 것이 괄호의 숫자가 항상 매칭되어야 하는데 이러한 괄호의 숫자를 맞추는 것은 재귀적으로 해야하고 이때까지 몇 개를 가지고 있고 이런 것들을 표현할 수 없기에 그대로 사용 불가능

→ Finite automata를 사용할 수 없다는 의미가 됨

Context free Grammars

4개의 컴포넌트로 구성

terminal symbol – 실제 알파벳이거나 토큰 스트림에서 받을 수 있는 토큰 하나를 의미 or empty string

Nonterminal symbol – 다양한 토큰들을 커버할 수 있는 변수(syntactic variable)

Start symbol – 시작점에 시작되는 nonterminal symbol(special nonterminal)

Production rule – 왼쪽에서 오른쪽으로 가는 것, 왼쪽은 항상 하나의 nonterminal 이고 오른쪽은 terminal과 nonterminal의 string, 믹스도 가능(LHS → RHS)

Nonterminal들이 어떻게 expand할 수 있는지를 판단

• 어떤 CFG으로 만들어지는 languages는 start symbol에서 production rule을 반복적으로 적용해서 터미널(토큰)들로 이루어진 set of strings of terminal를 의미한다
  • 귀납적으로 적용해서 만들어 질 수 있다면 그 grammar가 만들어질 수 있는 Language에 들어갈 수 있는 것을 알 수 있다.

L(G) = Language generated by grammar G

ex) CFG example

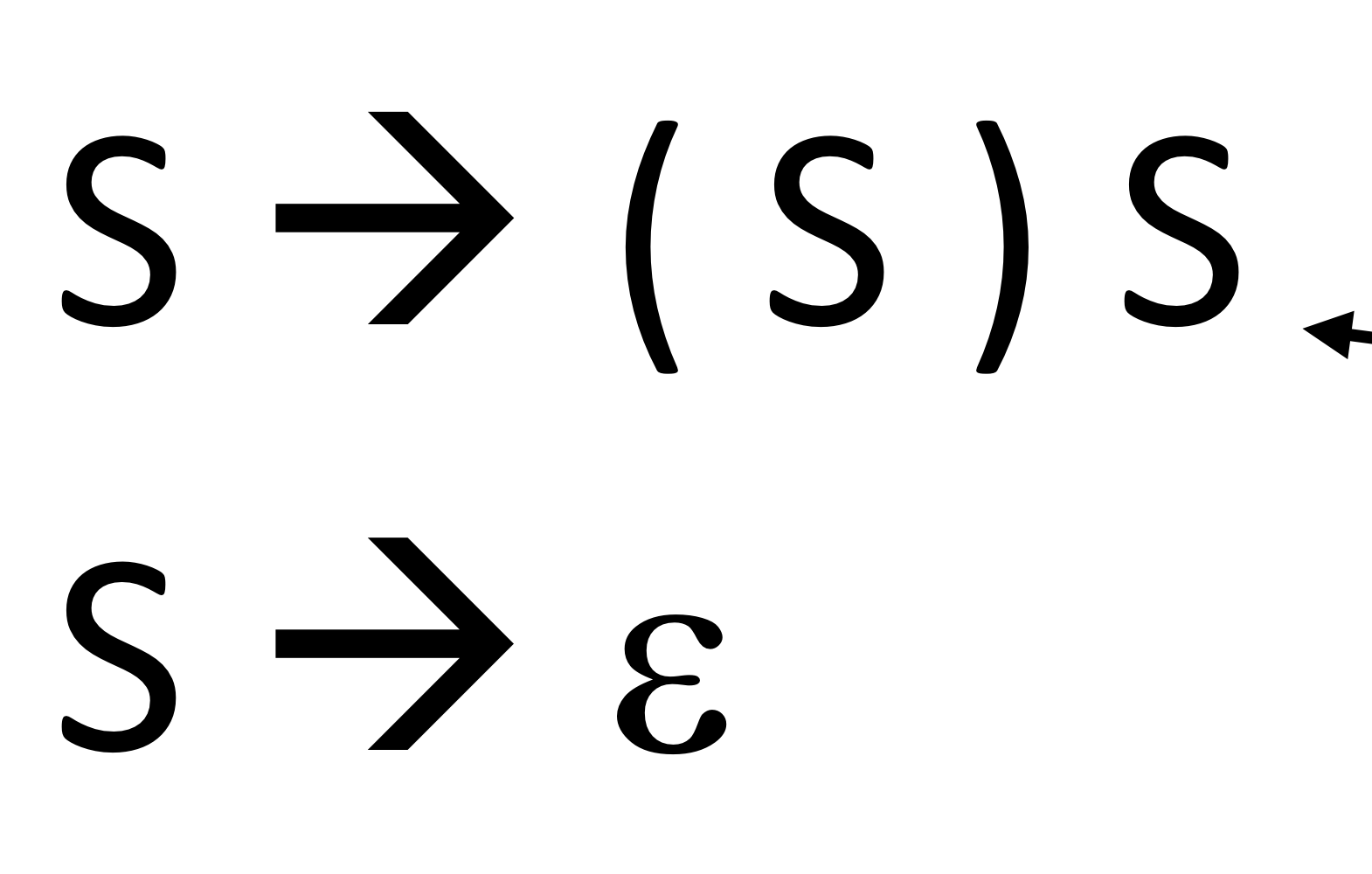
RE에서는 표현하기 힘든 괄호를 표현

cf. 뒤에 s가 생기는 이유는 뒤에 괄호가 또 생길 때를 대비하기 위함

S는 empty가 될 수도 있음

• 어떤 grammar가 string을 받아들인다는 것은 grammar rule에 의해 string을 production rule로 만들어줄 수 있는 derivation이 존재한다는 것

→ 이 string이 도출될 수 있다면 문법적으로 오류가 없음을 의미

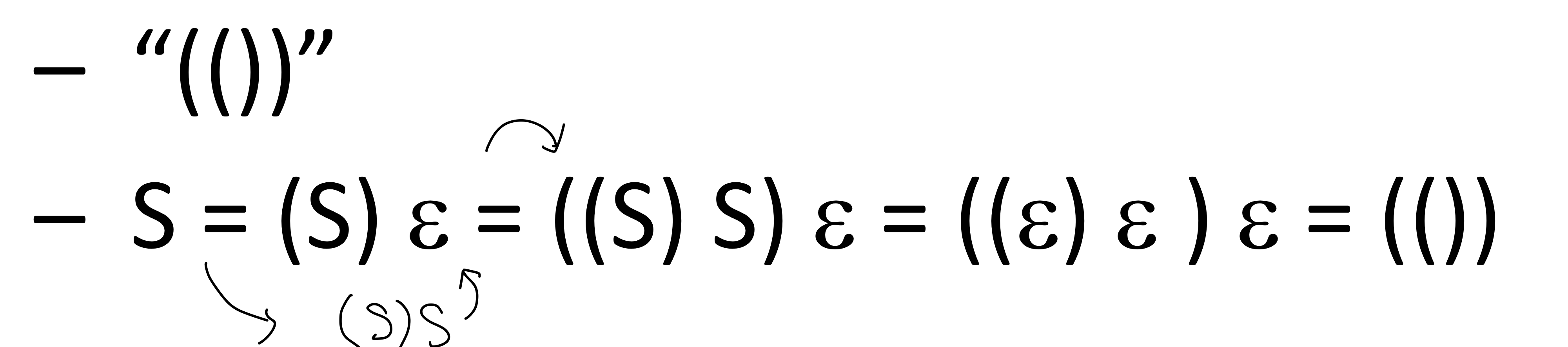
more on CFGs

• Vertical bar로 여러개를 간단하게 표현할 수 있다 :

• CFG는 대부분의 문법을 표현할 수 있으면 derivation으로 증명 가능
  • derivation : successive applicaiton of productions starting from S, start sybol부터 production rule을 연속적으로 적용하는 과정
• Input token stream이 derivation할 수 있다면 accept

Parser

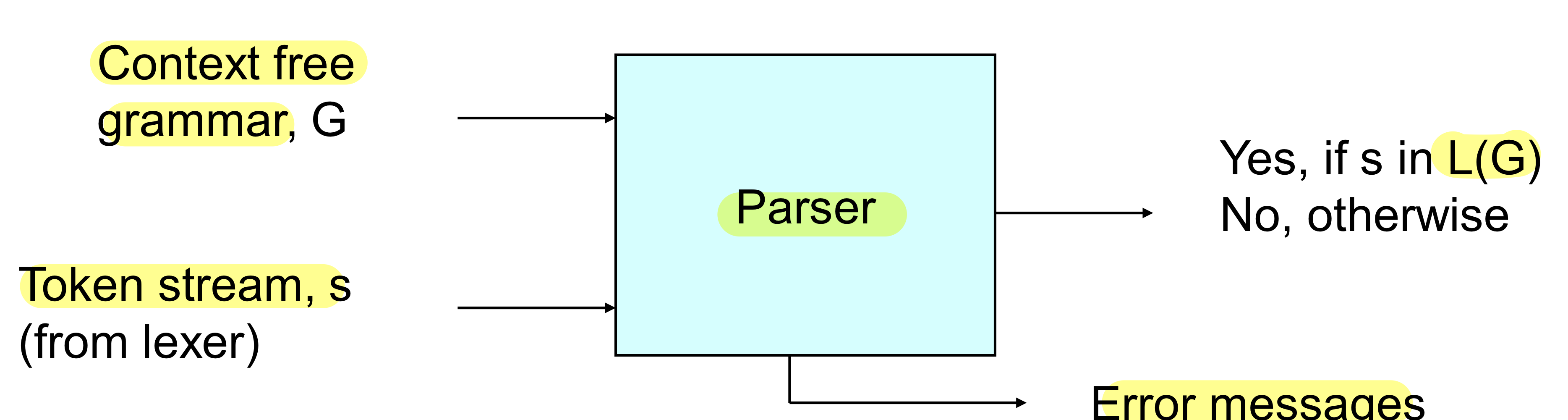
Input으로 CFG로 스펙을 지정해주고 이거에 따른 parser를 만들게 되면 token stream이 start symbol로부터 derive가 되면 문제가 없고 문제가 있다면 에러메세지를 출력

• CFG acceptor(Syntax analyzer, parser)를 만드는 것이고 token stream이 accept될 수 있는 derivation을 만들어주는 것
• DFA보다는 훨씬 복잡한 편, 더 많이 커버하고 해야 하는 일이 많기 때문에 이를 쉽게 하기 위해 LL(k),LR(k),SLR,LALR 등등이 존재하고 각각 방법에는 장단점이 존재
• 문법체크를 하는 것, CFG를 parser의 input으로 주고 CFG룰에 따라서 토큰 스트림을 검출하는 프로그램이 만들어진다. 토큰스트림은 문자열들의 모임인데 하나씩 읽어서 derive할 수 있는 지 체크해서 이 스트림이 grammar를 만들 수 있는 language라면 저장, 중간에 에러가 난다면 에러 메시지를 출력, 토큰 스트림이 accept된다면 그 derivation 결과를 저장하는 프로그램을 parser라고 한다.

RE is a subset of CFG

RE보다 CFG가 powerful하다는 것은 RE를 CFG로 표현할 수 있어야 한다.

ex) sum expression CFG

cf. 위의 예시는 실제 덧셈의 과정과 달리 왼→ 오른쪽으로 계산하는 것이 아닌 반대로 오른쪽부터 계산한다(오른쪽 부분이 더 derive되는데 오래걸리기 떄문에 더 먼저 계산하게 된다)

틀린 문법은 아닌 통념과 다를 뿐!곱셈은 덧셈보다 빨리 해야한다. (왼→ 오 순서로 계산해야 한다는 통념일 뿐)

right associate하며 나중에 나올 수록 우선순위가 높기 떄문에 +보다 ()가 나중에 나오는 것, syntax tree의 depth가 깊어질 수록 계산을 더 빨리 하게 된다.

nonterminal이 두개는 괄호와 덧셈의 우선순위를 맞추기 위함

production rule을 더 많이 거쳐야 높은 연산이 나올 수 있도록 한다 derive하는데 오래 걸릴 수록 계산은 더 빠르게 하게 된다. 반대니까!

Constructing a Derivation

• Start symbol인 S부터 시작
• sequence of token을 derive하기 위해 production을 사용
• A→ b production 시(a,b,r는 terminal+ nonterminal인 arbitary string을 의미, A는 nonterminal)
  • aAr → abr(A 대신에 b를 넣는다)

cf. deterministic하다면 항상 똑같이 나와야 하고 만들 수 있는 path가 오직 하나이지만 deterministic하지 않다면 계산순서가 달라진다 : ambiguous grammar

Parse tree

: derivation하기 위해 production rule을 하나씩 적용하게 되는데 기본적으로 derivation 시 과정을 트리로 보여주는 것

• tree representation of the derivation

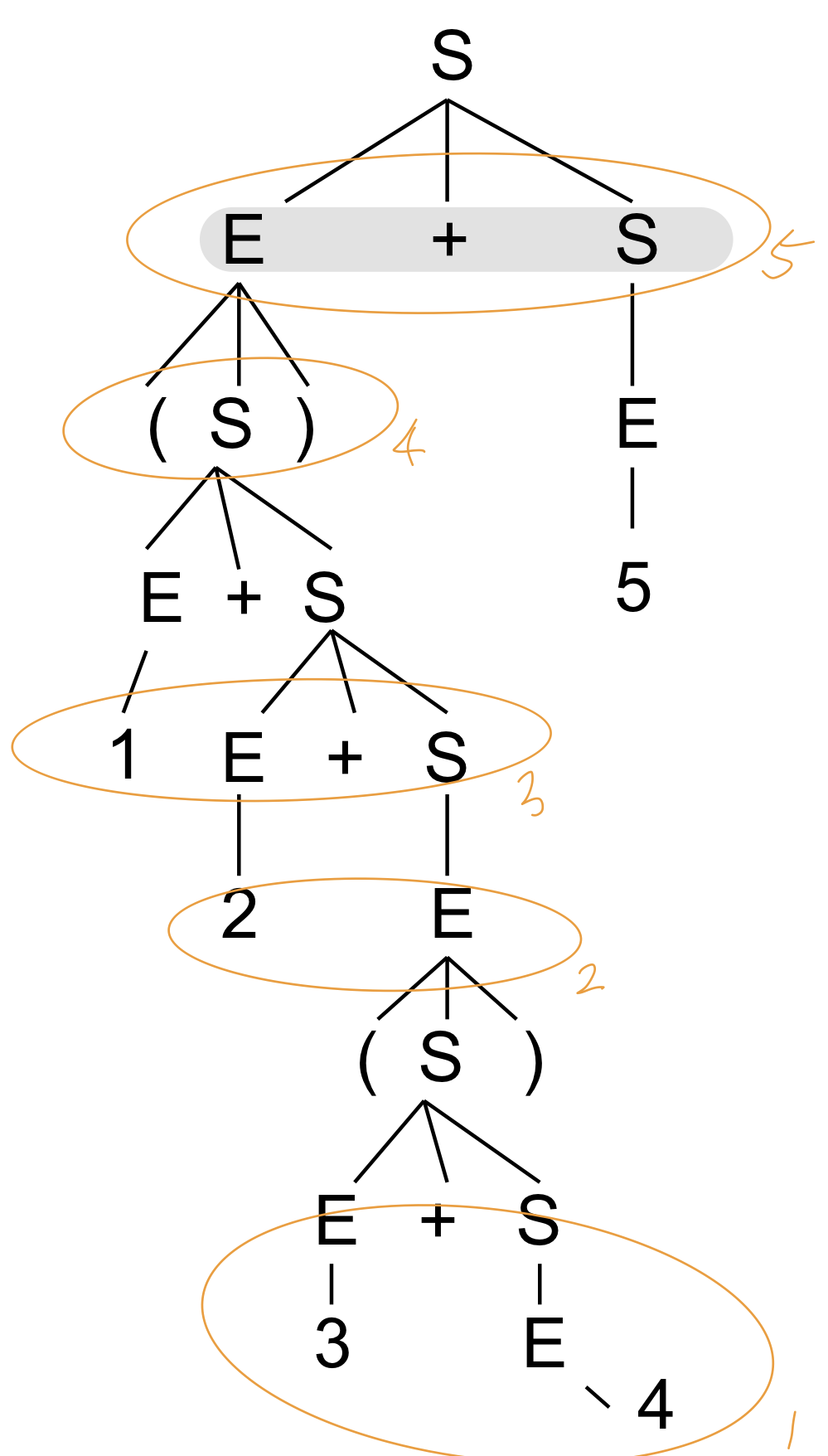
• 각각의 parse tree의 마지막 노드는 모두 terminal이고 nonleaf node는 nonterminal이다
• 적용한 순서는 저장되지 않는다(derivation step의 순서는 저장 x)
• 둘 중에 머가 먼저인지는 모르지만 어떤 과정을 거쳤는지는 알 수 있다

← 예시는 오른쪽부터 계산하는 것을 알 수 있다.

• 중요한 점에는 parse tree를 이용해서 문법적으로 어떻게 만들어졌는지 알고 결국 연산 순서를 알 수 있게 된다. Grammar를 잘 지정해서 토큰 스트림을 문법적으로 오류가 없는지 그리고 연산순서를 문법에 의해서 지정할 수 있다.
• derive가 늦을 수록 우선순위가 높은 편, 과정을 그래프 형태로 저장하면 parse tree가 된다. nonterminal의 production rule의 순서를 표현하며 계산한다는 것은 token stream으로 최종적으로 s를 만드는 것이라고 볼 수 있다.

Parse tree(concrete syntax) vs Abstract syntax tree

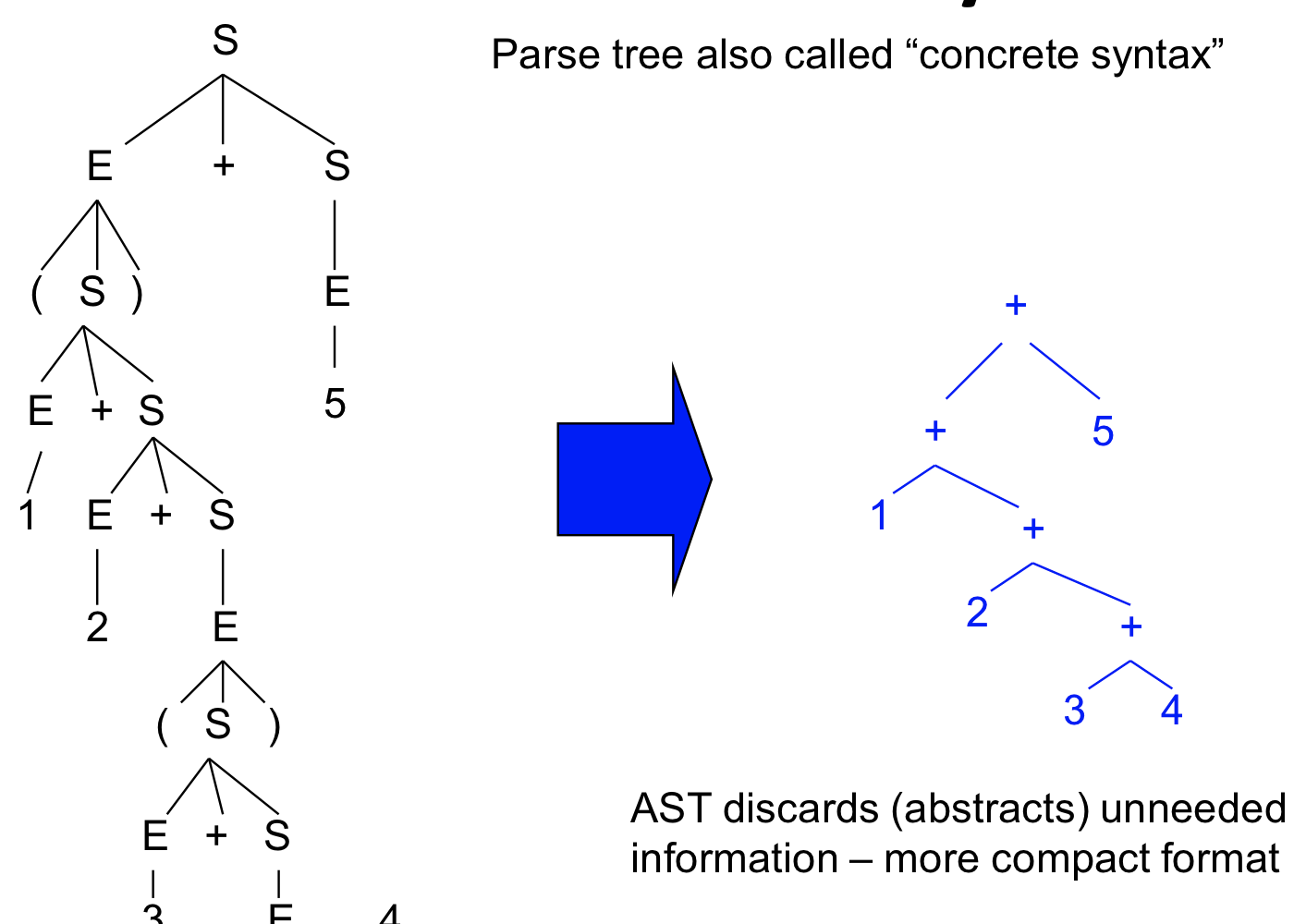
Parse tree에서 중요하지 않는 부분을 지우는 것이 abstract syntax tree이며 프론트 앤드를 거쳐서 프로그램의 의미만 남길 때 이렇게 저장함

cf. 프로그램을 만들고 어셈블리로 만들어줘야 하는데 최적화를 하려면 트리의 노드 수가 작은 것이 좋기 때문에 괄호가 사라질 수 있다.

(정리)

lexical structure은 regular expression로 표현하고 syntatic structure은 context-free grammar로 표현한다.

CFG는 grammar rule의 set이며 RE와 CFG의 가장 큰 차이는 recursion을 제공

S에서 시작해서 반복적으로 production rule을 적용하는 것이 derivation

derivation이 존재한다면 acceptance이다.

나의 CFG가 deterministic하다고 할 때 잘못된 길로 빠지지 않도록 가이드해주며서 파싱을 수행하는 작업이 parsing scheme ex) LL, LR, LALR, SLR

Derivation Order

Parsing을 할 때 derivation해서 input token stream을 만드는데 derivation order는 저장되지 않는다.

→ Derivation 순서를 정하는 것이 더 편할 수 있다.

왼쪽에서 오른쪽으로 derivation 할 때 순서를 정하면 체계적으로 derivation할 수 있다

• left most(leftmost nonterminal부터 production 적용) → LL

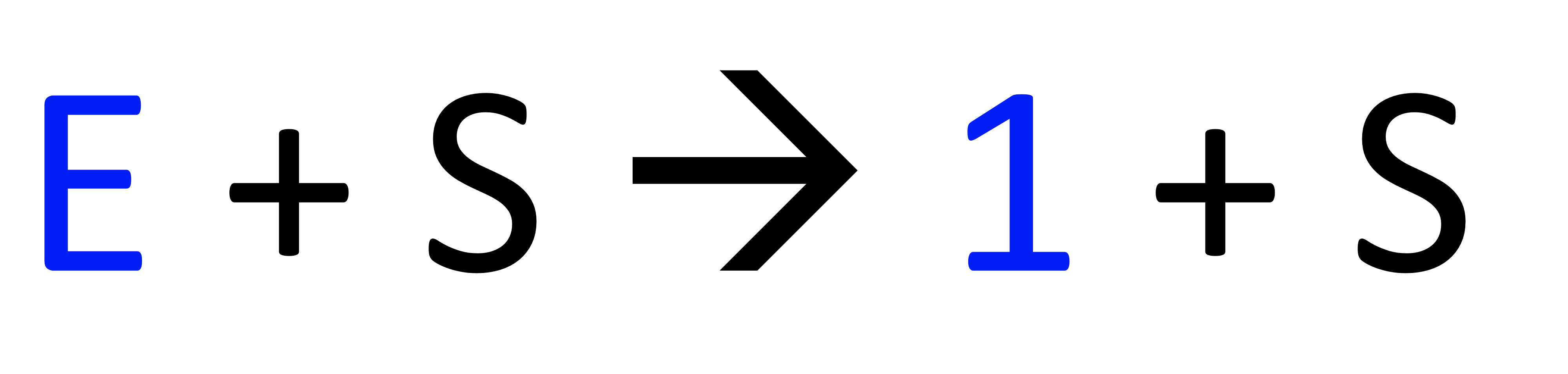
• right most(rightmost nonterminal부터 production을 적용) → LR

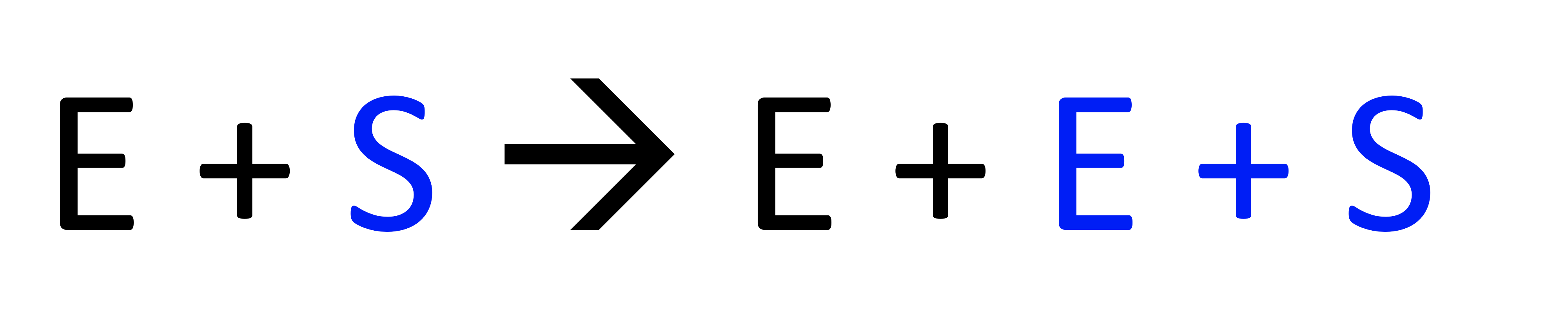
둘 다 해도 같은 parse tree를 만들게 되고 같은 production이 선택되지만 순서가 다르며 이 두 개 꼭 해보기

Left most와 right most의 결과는 무조건 같아야 하고 어떤 parser를 선택하든 똑같은 결과가 나와야 한다. 다른 경우도 있는데 이는 애매모호하게 CFG를 정해서 생긴 것

ex)

cf. e→e+s도 있고 e→e도 있는데 왜 e→e로 갈까? multiple choice가 존재할 때 머부터 적용해야하는지 알려주는 것이 parser

Ambiguous grammar

Leftmost, right most derivation에 따라서 결과가 달라지는 문법을 의미

sum expression의 경우)

우리가 만든 애는 괄호가 없는 경우에는 오른쪽부터 만들어진다. 덧셈을 오른쪽부터 계산하게 된다 다 오른쪽으로 만들어지게 된다.

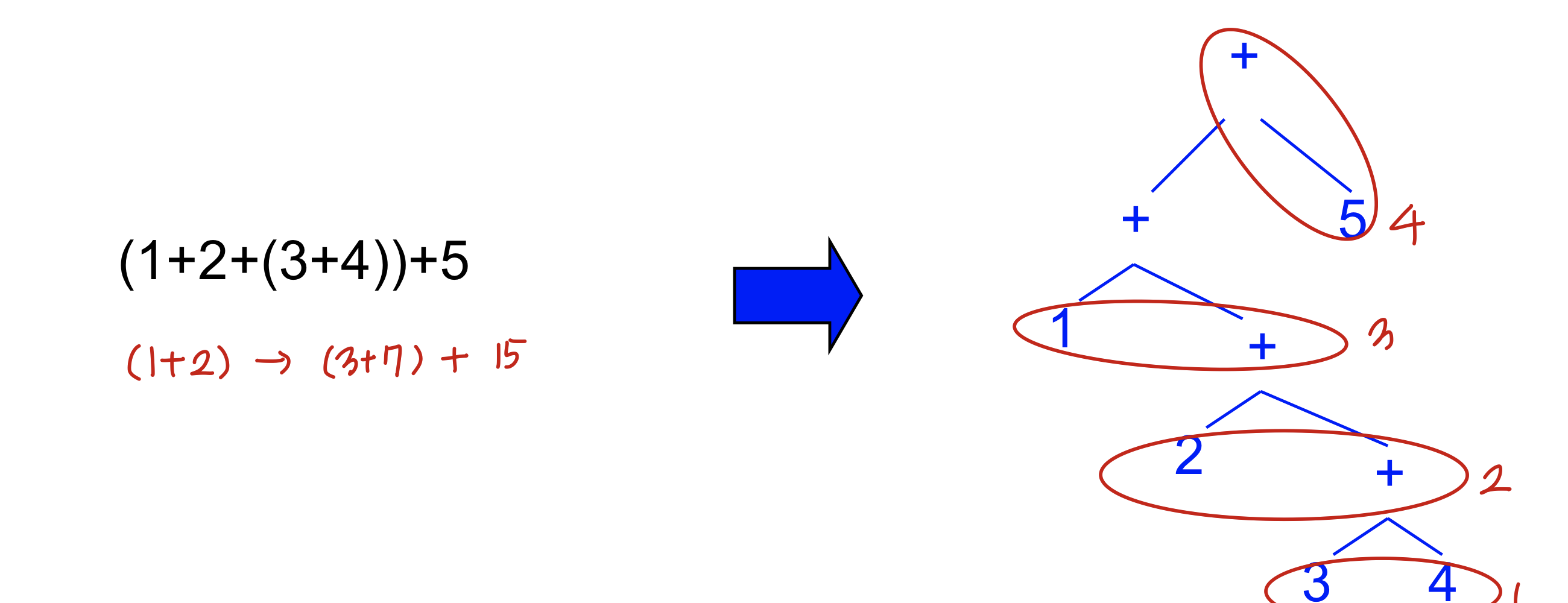
이게 우리가 생각하는 것과 다름, 우리는 주로 associate to left인데 얘는 right임

• 왼쪽으로 바꿔줘야 한다. 하지만 애매모호한 것은 아님 왜냐면 동일한 결과를 만들어주기 때문
• 틀린 grammar는 아니지만 원하는 그래마는 아닐 수 있다.
  • S→ E+S로 변경한다면 associativity가 만족될 것, 오른쪽이 커진다
• leftmost와 rightmost derivation이 identical parse tree를 만들기 때문에 애매하지 않은 문법임

애매한 문법의 경우)

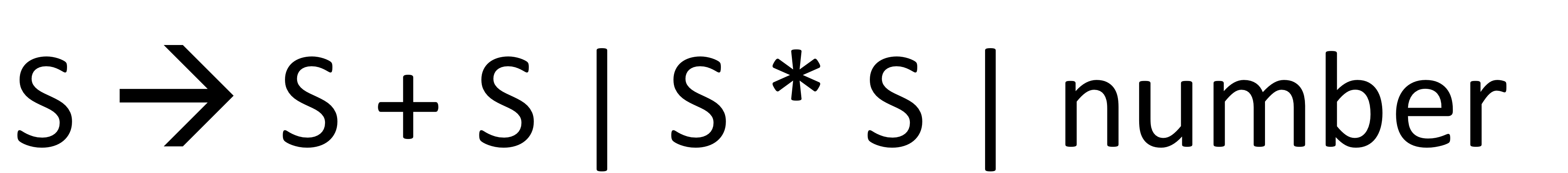
• Leftmost와 right most parse tree가 다른게 ambiguous grammar
• E를 없애게 된다면 ambiguous가 생기고 parse tree가 여러개 생기게 됨

S와 s중에 expand가 머가 될까? 또 s*s와 s+s가 있으면 머가 먼저 수행되는지 애매하다

→ 수정해줘야 한다

어떻게 수정해야 할까??

→ associativity가 한방향이 되도록 하고 우선순위를 잘 지정한다면 애매하지 않게 된다.

→ Grammar를 잘못만들기 때문에 잘 만들어주면 된다!

ex) ambiguous grammar의 예시

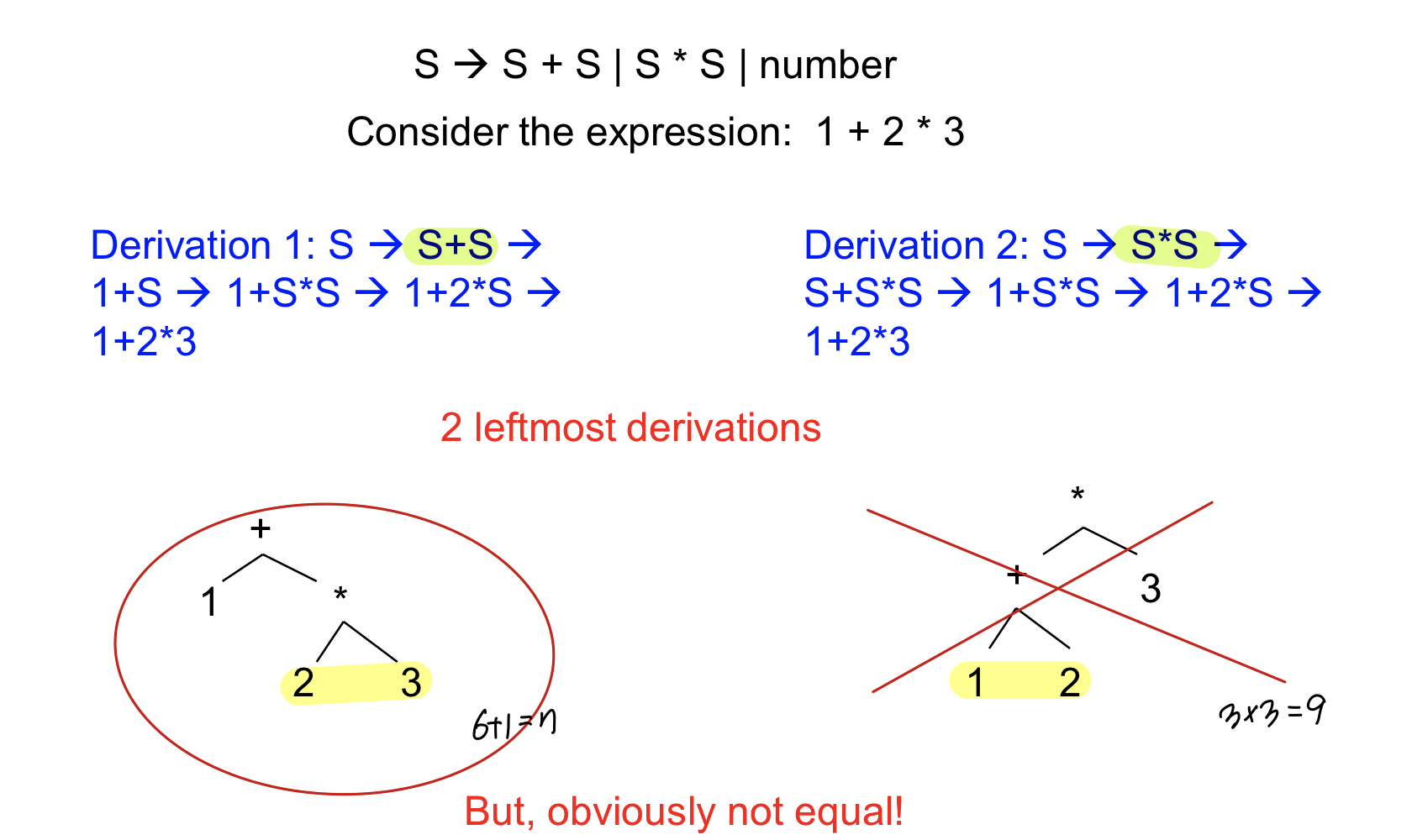
위와 같이 다른 parse tree는 다른 결과를 나오게 할 수 있게 된다.

✅Eliminating Ambiguity

ambiguity는 문법을 잘못 지정한 것이기 때문에 문법을 고치면 된다

즉, 한쪽으로 커지게 정해주자!

1) 새로운 nonterminal을 추가해서 우선순위를 지정한다

2) 한방향으로만 recursion이 일어나도록 하게 한다.

ex)

T로 우선순위를 만들어주게 되고 왼쪽으로만 커지고 커지고 왼쪽부터 계산해주도록 한다

→ S가 왼쪽에 있으므로 왼쪽으로 커지는 거고 T를 만들어서 우선순위를 만들어 덧셈과 곱셈 중에 곱셈 먼저 한다.

Derive를 먼저하는게 우선순위가 낮아지는 거임

Leftmost이든 rightmost이든 똑같은 값이 나오게 된다.

Precedence enforced by

• 연산순들의 우선순위 레벨에 맞는 각각의 nonterminal을 만들어준다.
• 각 레벨에 맞춰서 production rule을 만들어준다.
• 우선 순위가 높은 애는 다음으로 높은 nonterminal에 의해서 만들어지도록 한다.
• higer precedence는 더 나중에 나오게 된다

Associativity

• 연산자들은 각각 왼쪽이나 오른쪽, 없는 경우도 존재, 덧셈은 left, 지수는 right인데 이걸 주기 위해서는 recursion으로 줄 수 있다. Left recursion이라면 left associativity임

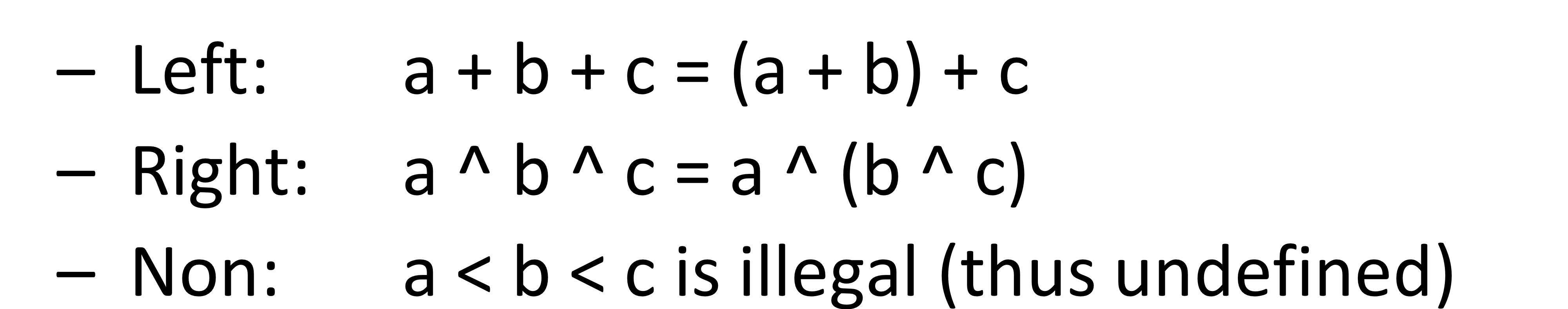
• recursion의 위치는 operator의 associativity를 의미
  • left recursion → left associativity
  • right recursion → right associativity
• common sense와 상관없이 associatiivty를 지정해주는 것이 중요

오르쪽이나 왼쪽으로 recursion을 인가하도록 한다

• 연산들의 우선순위를 만든다 : 각각의 새로운 nonterminal을 만들어주고 우선순위에 따라서 Production rule을 만들어준다. 우선순위가 높은게 다음 nonterminal을 이용해서 만들어주도록 하면 된다

Bison Overview

lexical analysis에 flex가 있는 것 처럼 syntax analysis에는 parser를 만들어주는 프로그램이 있고 그것이 바로 bison

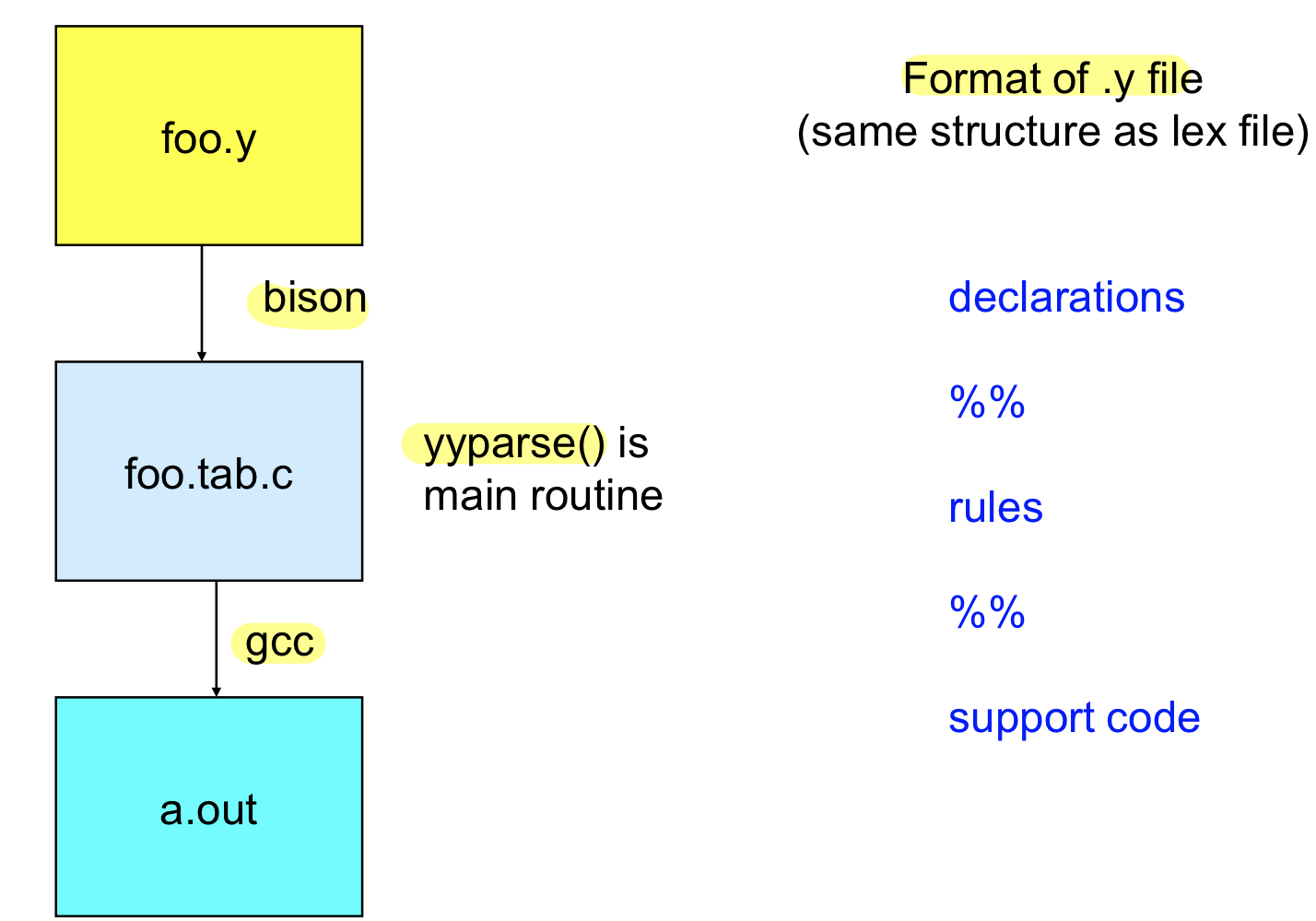
• 파싱하는 structure을 넣어주면 parsing하는 yyparse()라는 c파일이 나오고 이걸 컴파일하면 ㅠㅏ서가 만들어진다

declaration section

• start symbol과 associativity(left, right, none)와 우선순위를 지정
• attribute value
• symbol attribute

values used by yyparse()

• erro function
• last token value YYSTYPE
• setting yylbal in flex

→ yylval이 사용가능해진다

rule section

• production을 표현하고 action을 표기

attribute value

conflicts

• bison은 shift/reduce reduce/reduce conflict이 일어날 수 있다.
• CFG가 Ambiguous하다는 것은 conflict이 일어난다. Ambiguous는 parse tree를 만들 수 있는 게 여러 개 나올 경우 conflict이라고 한다. 여러개의 경우의 수가 나온다. 바이슨에서 기본적으로는 문법이Unambiguous하게 지정되어야하지만 항상 그렇게 되기는 어렵기 떄문에 conflict가 났을 때 그냥 이쪽 방향이 맞겠구나 선택해서 별 문제 없이 파싱되게 하는 방법을 사용한다.(shift- reduce conflict, reduce-reduce conflict)
• Regular는 무조건 되지만 CFG는 ambiguous한게 만들어질 수 있고 그 때에도 잘 derive가 될 수 있도록 conflict가 났을 때 bison에서만(lr parsing)해줄 수 있는 룰을 지정해주게 된다.

bison은 lr parsing을 이용해서 만든 프로그램임.