== predictive parser, LL parser

Parser의 종류가 다양하다고 했는데 그 중 top down parser를 볼 것

Topdown, bottom up parser 등등 많음

CFG parser(syntax analysis)는 lexical analysis보다 복잡하고 완벽하지 않기 때문에 다양한 편

• 간단하지만 커버리지가 적은 편인 top down parser
• 복잡한 대신 커버리지가 많은 편인 bottom up parser

LL parser(top down parsing)은 derivation 시 멀 먼저 해야할까에 대한 결정에 흰트를 준다.

Parsing Top-down

Token을 하나씩 읽으면서 CFG를 leftmost derivation하는 것

• Input token stream을 읽어가면서 leftmost derivation하고 모든 토큰 stream을 읽을 때 까지 derivation이 된다면 문법적으로 오류가 없음을 이해 가능
• 간단하지만 커버리지는 않좋은 편

cf. 덧셈은 왼쪽으로 assosicate이긴 하지만 얘는 오른쪽으로 associate이고 애매모호한 CFG는 아님

괄호임으로 (S)로 변경 -> e를 1로 변경 -> …-> 토큰을 읽어가면서 derivation을 적용해서 문제없이 토큰 stream을 파싱할 수 있다면 문법적으로 문제가 없음을 알 수 있다

여기서의 힌트는 가장 최근으로 본 토큰과 현재 나의 nonterminal을 이용해서 지정하는 것이 LL parser임

lookahead - 검출하지 못한 토큰의 제일 왼쪽에 있는 부분

                                                                                                                                                                                                                                                                                                                                                                                                                                        parsed part - 이미 만약 나중에 derivation으로 완벽하게 적요된다면 문제없이 봤다고 파싱했다고 생각하는 부분

unparsed part - 아직 파싱이 안된 부분

하나의 토큰을 보고 옵션 중에서 고를 수 있다

Problem with Topdown parsing

다음 심볼이 있을 때 어떤 production rule을 적용해야 하는지 모를 경우가 존재

Ex) e+s로도 갈 수 있고 e로도 갈 수 있지 않는가? Ex1이라면 s->e로 가야하고 ex2라면 e+s로 가야 한다

but 왼쪽괄호만 보고 있기 때문에 우리는 무슨 production rule을 적용해야 할지 모르게 된다

grammar is problem

⇒ grammar가 문제이다! : 스펙은 맞지만 topdown parser에서는 정확하게 작동되지 않을 수도 있다는 의미

• 맨 왼쪽의 하나의 심볼을 봐서더라도 두개 중에 어떤 production rule을 정할 수 없다 == LL(1) g rammar가 아니다!!
• LL(1) = left to right scanning, left most derivation, 1 look ahead symbol
  • 토큰을 왼쪽부터 오른쪽으로 스캔하고 가장 왼쪽부터 derivation하고 하나의 lookahead symbol을 보았을 때 파싱이 가능한 경우
  • LL(K) = lookahead symbol을 여러개 보는 경우

문법은 나름 맞게 만들었지만 하나의 lookahead를 보고는 파싱할 수 없다 즉, ll1 grammar가 아니다

⇒ LL(1) grammar로 바꿔줘야 한다 : Left factoring, left recursion elimination 두가지 방법으로 LL(1) grammar를 만들어주면 top down parser를 만들 수 있어진다.

• 어떠한 parser는 커버리지가 좋고 나쁨이 있는 이유는 top down에 맞는 grammar의 형태가 한정적이기 때문
• 그러나 top down parsing은 가볍고 빠른 편이라서 간단한 문법에는 자주 사용함

LL(1)

• 토큰을 왼쪽부터 오른쪽으로 스캔하고(left to right scanning)
• 가장 왼쪽부터 derivaiton하고(left most derivation)
• 하나의 lookahead symbol을 봤을 때 파싱이 가능한 경우를 의미(1 lookahead symbol)

cf.LL(k)는 look ahead symbol을 여러개 보는 것, 하지만 보통은 ll(1)을 주로 사용함

⇒ 정의한 grammar를 ll(1) grammar으로 변경해야 한다.

✅Making a Grammar LL(1)

1) Left factoring(right recursive grammar에 적용)

: Right recursive에서 문제가 있을 때 left factoring으로 해결

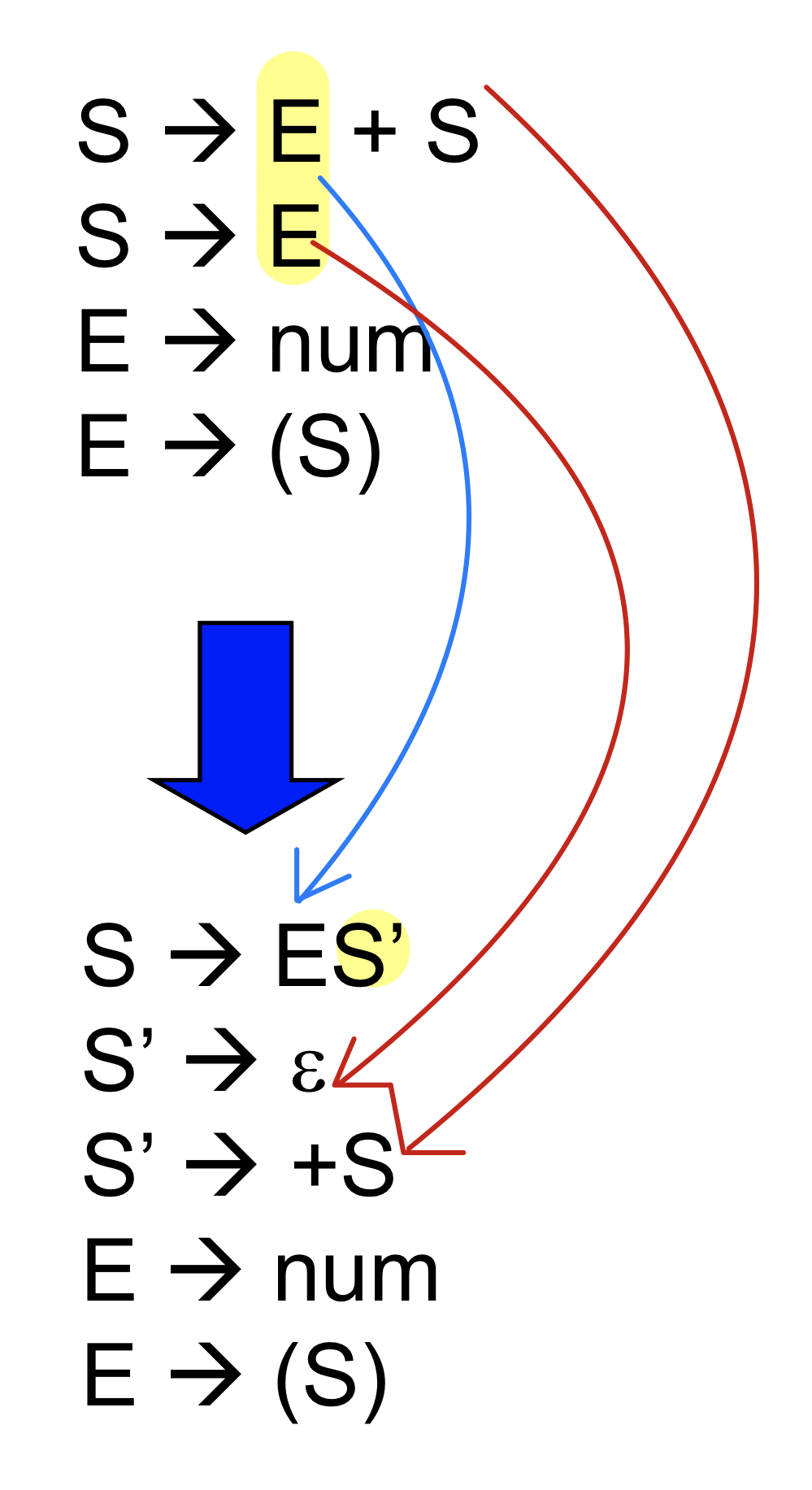
• S가 e로도 혹은 e+S도 갈 수 있는데 e로 갈 때 뒤에 +s인지 볼 수 없다

→ 주어진 문법은 right recursive이므로 grammar이므로 left recusion elimination은 필요하지 않으며 left factoring을 수행한다.

• 뒤에 +s이 올 수도 있고 없을 수도 있으니까 e를 묶어서 하나의 production rule을 만들고 나머지를 묶는 것
  • 같은 아이들을 묶고 나머지 아이들을 새로운 nonterminal s’로 만들어주는 것

  → S’로 무조건 간 후 그 뒤에 결정하면 되므로 해결 할 수 있게 된다

• 주어진 grammar는 덧셈과 괄호 사이의 우선순위도 잘맞고 association도 하나로 잘 지정되지만 LL1 parsing하기에는 어렵기 때문에 left factoring으로 공통적인 부분을 묶어서 하나로 만들어 e만 보고 결정할 수 없는 문제를 해결한다.

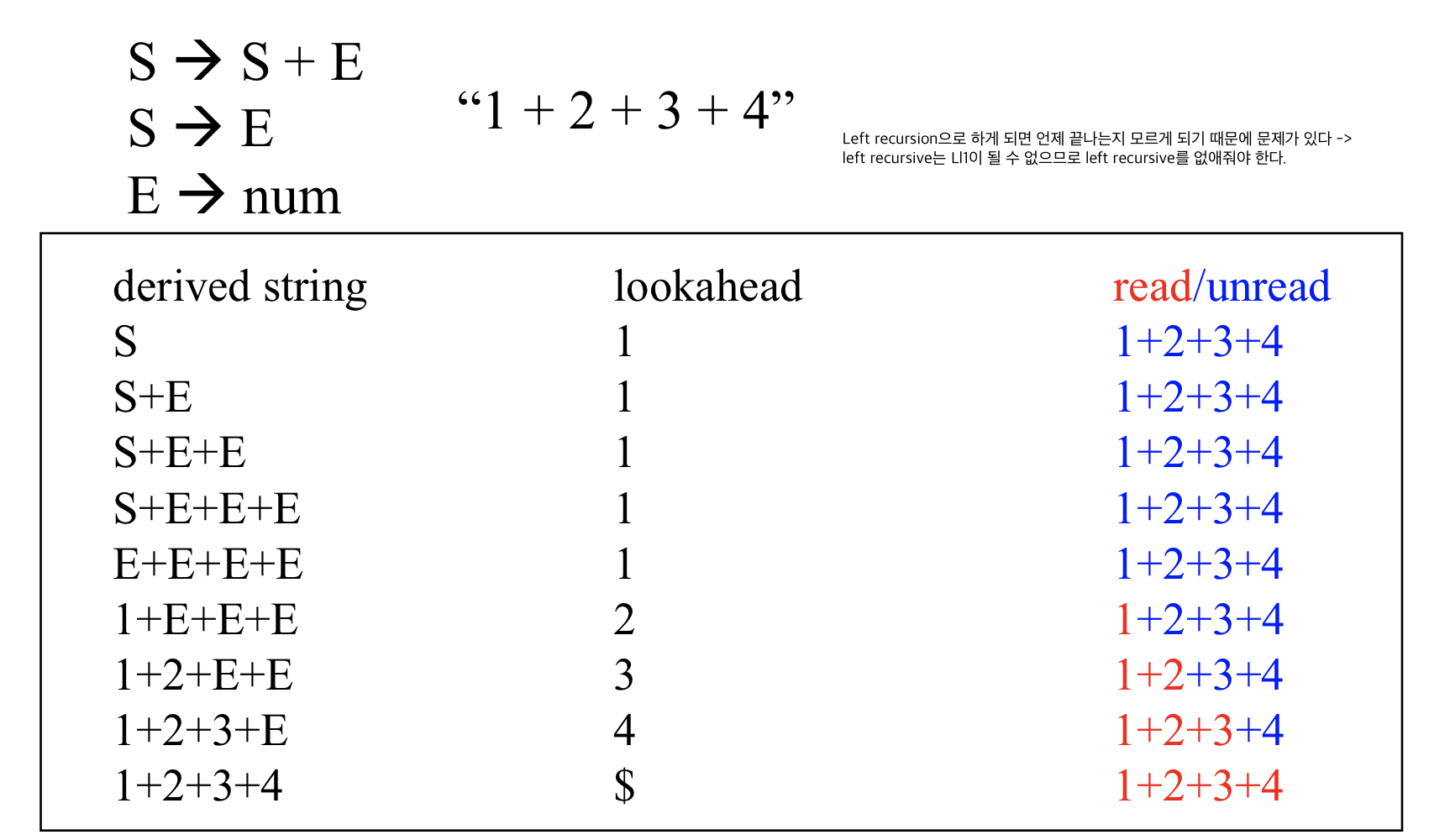
2)Left recursion elimination(left recursive grammar에 적용)

Left recursive인 경우에는 left recursion -> right recursion으로 바꾼다

• 주로 많은 문법은 left recursion grammar일 가능성이 높다.

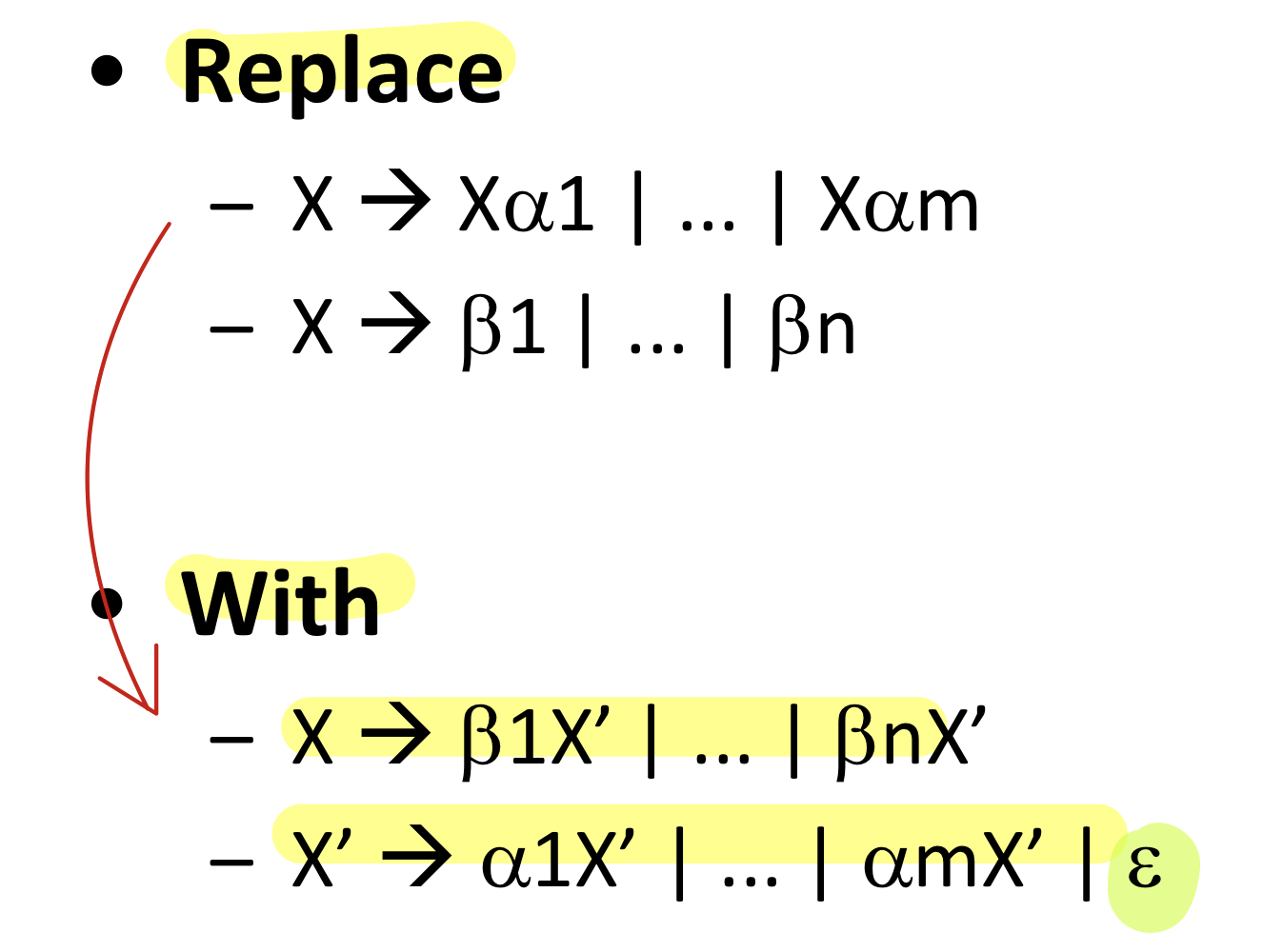
• 위의 방식대로 변환하면 된다. 기계적으로 할 수 있으면 된다. 꼭 알 것

→ LL(1) grammar로 변환 후의 parsing

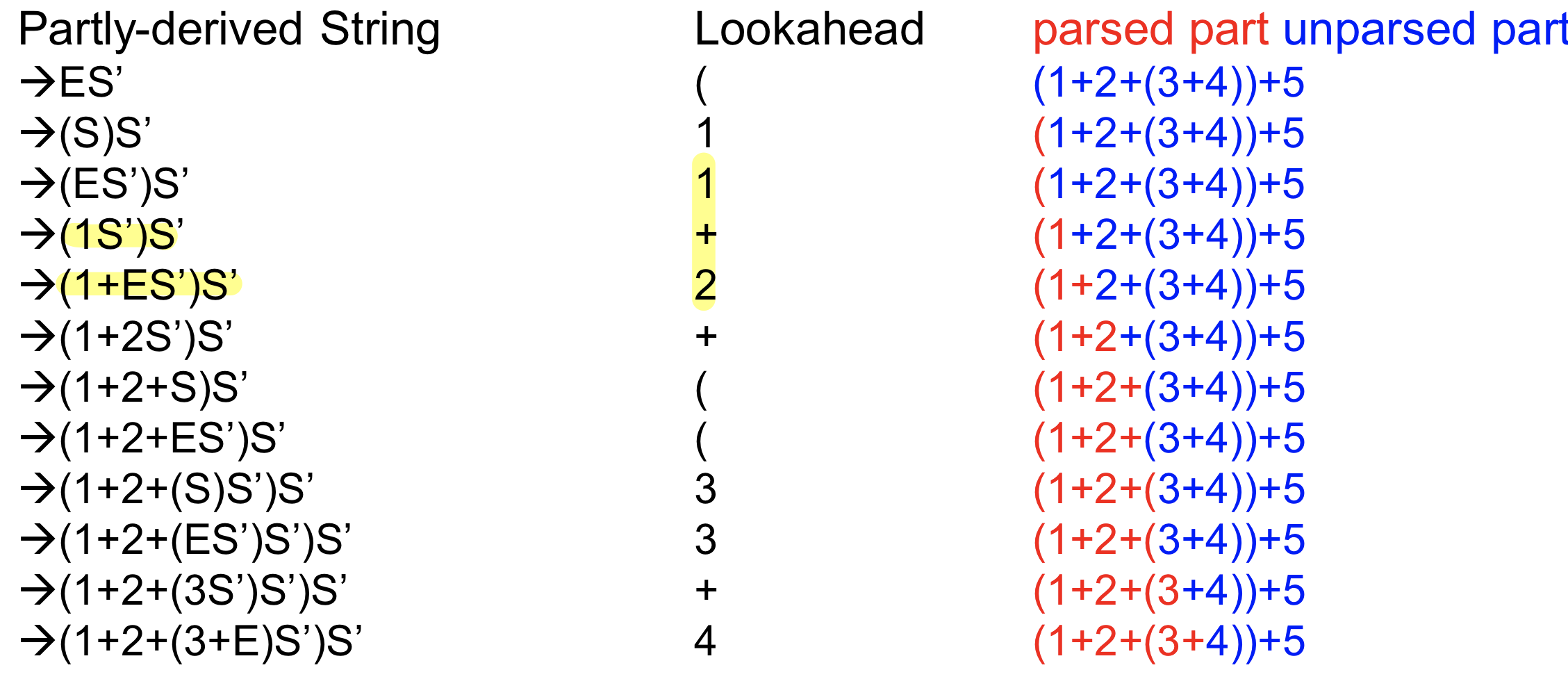
예시 중요

Predictive Parsing

: LL(1) grammar를 이용해서 top down parsing을 하는 것(== topdown parsing)

• Ll(1) grammar가 있을 때 하나의 lookahead symbol을 보면 production rule을 하나로 지정할 수 있고 ll(1)grammar를 이용해서 parsing하는 것
• Predictive parsing table을 이용해서 쉽게 만들어줄 수 있다.
  • non-terminals * terminals → productions
  • non-terminals 과 terminal(lookahead symbol)을 이용해서 production rule을 지정할 수 있게 된다.

Parsing with table

• Nonterminal이 있고 터미널이 있고 nonterminal은 production 왼쪽에 사용하고 얘는 loockahead symbol에 존재
• row는 nonterminal이고 column은 terminal이여서 각각의 production rule을 지정해준다.
  • terminal은 Lookahead symbol로 보면 되며 nonterminal은 지금 내가 가지고 있는 가장 왼쪽의 nonterminal을 말한다. 맨 왼쪽에 있는 nonterminal을 lookahead symbol을 봐서 매칭해서 production rule을 lookup해서 가면 된다.
  • 셀에 하나를 초가하는 수의 rule이 들어가면 문제가 있지만 하나 이하라면 문제가 없고 없다는 것은 derive할 수 없다는 의미로 문법 에러가 존재한다는 의미!
• Parsing은 $가 endmarker로서 끝남을 알려줌

ex) 위의 parsing table로 parsing하는 과정

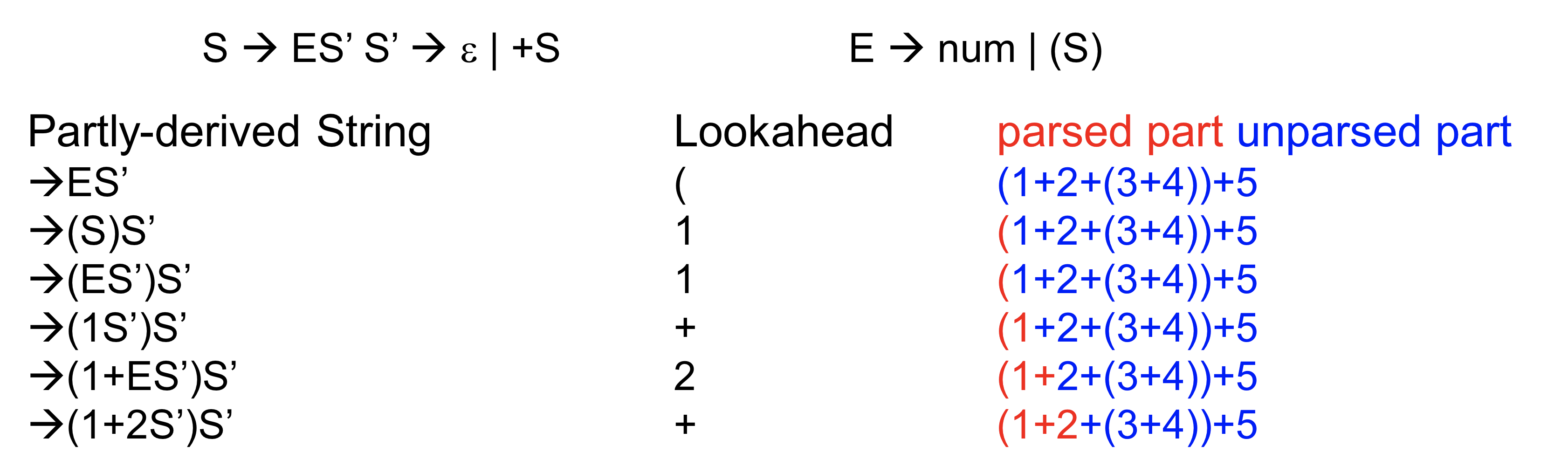
Parsing table로 실제로 Parsing하는 과정

실제로 Table이 있을 때 parsing을 실제로 어떻게 하는가?

• Table은 recursive descent parser(top down parser)를 만들어준다.
• Table에 의해서 parsing function이 만들어지고 parsing function은 nonterminal마다 하나씩 생성

ex) 위의 예시에서는 nonterminal이 S,E,S’ 세가지가 있으므로 parse_S(), parse_S’(). parse_E() 세개의 함수가 필요

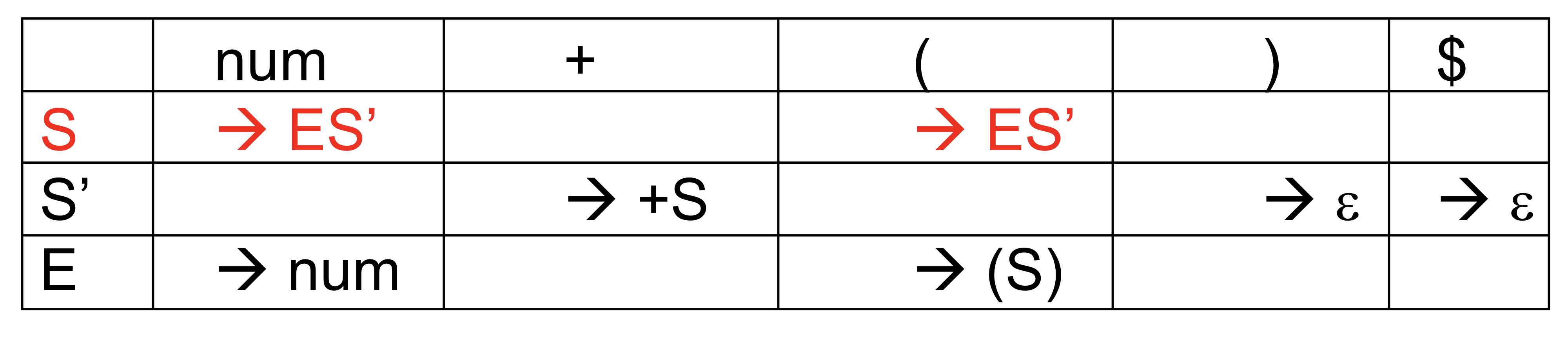
• Recursive descent parser라고 부르는 이유는 topdown parser로 부르게 되면 lookahead symbol을 보고 그거 에 따라서 parsing function을 recursive하게 부르고 이것이 문제없이 리턴된다면 오류가 없음을 알 수 있다

Call tree = Parse tree

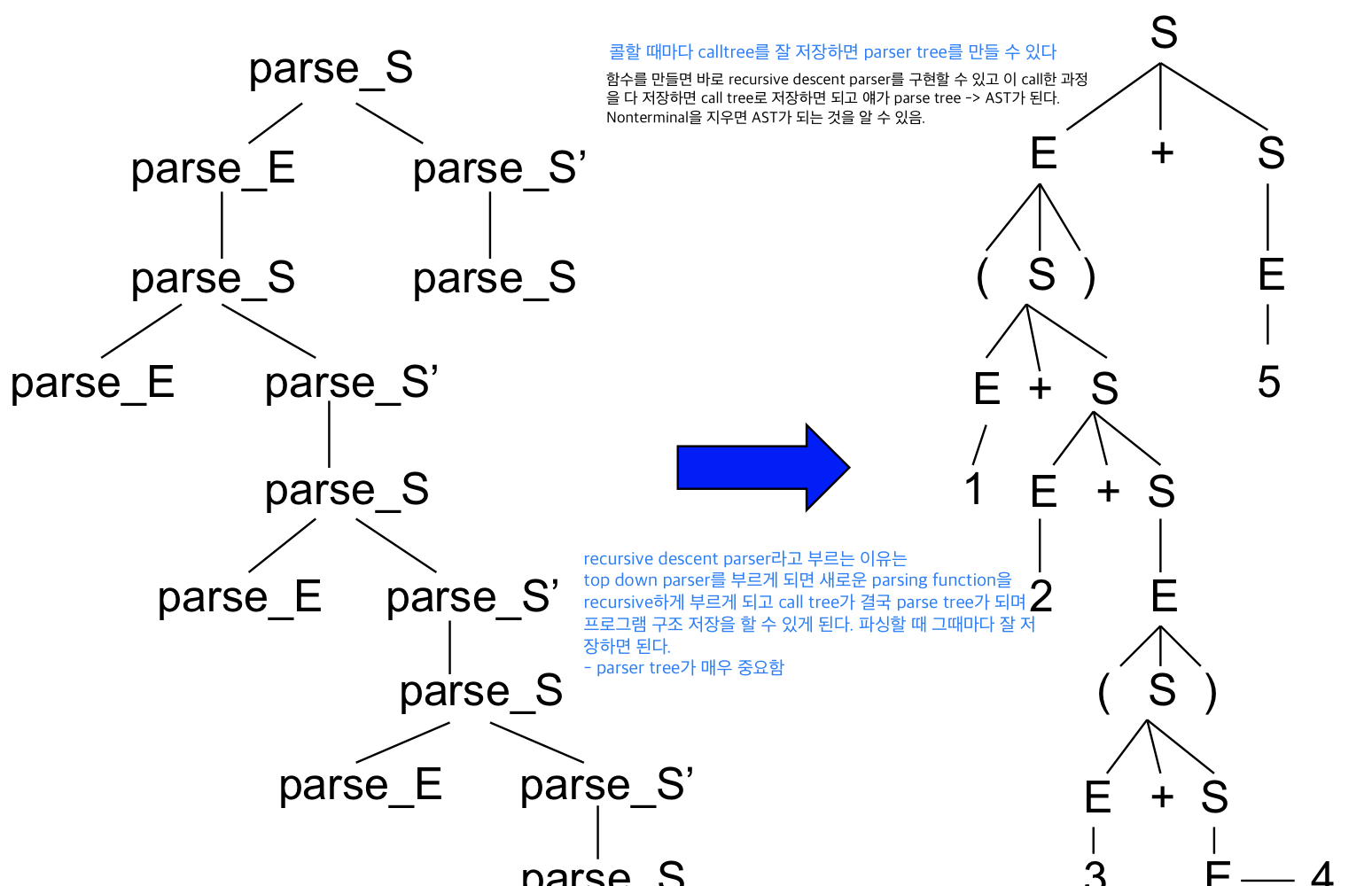
• call tree가 결국은 parse tree가 되고 이 프로그램 구조 저장 시 parse tree가 되고 이를 매번 호출 시 잘 기억하면 된다.
• parse tree에서 nonterminal을 지우게 되면 AST가 된다.

→ 정리 : call tree → parse tree → AST

Parsing table을 만드는 방법

• Grammar를 가지고 predictive parsing table을 자동으로 만들 수 있어야 한다. 기본적으로는 CFG가 ll(1) grammar이어야 한다. 아니라면 바꾼 후 table로 바꿔줘야 한다.

• 가능한 토큰들에는 무엇이 있을지 다른 lookahead symbol이 있을 떄 에러를 만들 것인지 등등을 알아야 함

⇒ 각각의 nonterminal에서 맞는 production rule을 수행할 수 있는 lookahead symbol을 찾는 것

• first(beta),follow(x)를 사용해서 찾는다
• 모든 nonterminal에서 lookahead symbol은 최대 하나의 production rule을 할당받아야 한다.
  • 두 개라면 문제가 되고 0개면 에러, 1개면 정상
  • 모든 nonterminal에 대해서 모든 lookahead symbol이 최대 1개의 production을 가질 경우 predictive parser를 만들 수 있게 된다.

  

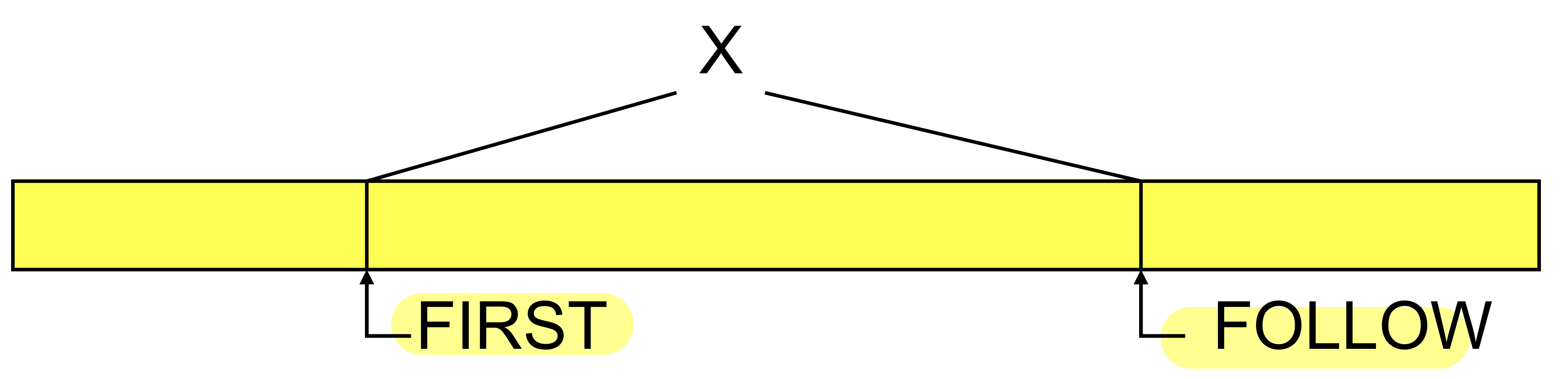
1) first(b)

어떠한 랜덤 string b(nonterminal + terminal, 내가 가지고 있는 토큰 스트림)가 있을 때 맨 앞에 있을 수 있는 terminal을 의미(symbol들의 모임)

b가 derivation되었을 때 가장 처음 나올 수 있는 심볼, terminal의 조합

First는 결국 x가 어떠한 production rule을 first 조합이 있을 때 수행해도 되는구나를 알게 된다. Production rule을 계속 적용하면 그 lookahead symbol이 나오니까!

ex) first에 +가 없는데 lookahead symbol이 +라면 문제가 있음을 알 수 있다!

2)follow(x)

X라는 nonterminal이 production rule로 커졌을 때 그 다음에 처음 나오는 심볼들의 모임

• First는 expand했을 때 맨 앞에 나올 수 있는 심볼, follow는 x가 expand(derivation rule로 커졌을 때)되었을 때 모든 string 다음에 처음으로 나오는 심볼들의 집합

→ 어떠한 string이 커지는데 결국 처음에 나오는 터미널을 first, 다 나온 후 그 다음에 나올 수 있는 심볼이 follow

→ 이 두가지를 사용해서 predictive parsing table을 만든다.

parse table entry

• x→b 라는 production이 있을 때 먼저 x row에 있는 first(b)에 있는 심볼들에 →b를 넣어준다.
• 만약, b가 nullable이라면 follow(x)에 있는 심볼들에 →b를 넣어준다.

(이유 : 다 없어진 다음에 첫번 째로 나오는 심볼일 것이기 때문)

• Ll1에서는 하나의 칸에 두개 이상의 entry가 없는 경우 LL(1) grammar라고 볼 수 있다.

x-> 베타일 경우 베타가 엄청 커지게 되면 첨에 first가 나오게 되고 만약에 베타가 nullable이라면 베타가 끝난 후 처음 나오는 심볼을 의미하고 얘는 follow : production rule을 추가하면 된다

(주의할 점)

• es’의 first와 e의 first는 여기서는 같지만 e가 Nullable이라면 다를 수 있다.
• X를 가지고 first x를 보면 lookahead에 그게 있다면 lookahead symbol에 따라서 가면 되는 것이고 first에 지금 보는 심볼이 없다면 얘는 production을 수행하면 안되는 것
• Lookahead symbol은 parsing할 X는 결국 derive하다보니 제일 먼저 만나게 되는게 first니까 보는 것 Follow는 x가 null인 경우 그 다음에 제일 먼저나오는 것이므로 follow 안에 lookahead sybmol이 있는지 봐야 한다.

Ex) x-> b라는 production rule이 있을 때 X의 row에 b의 first 부분의 셀을 →b로 채워주면 된다 First(es’)에 num이 있다면 num에 es’를 채워주면 된다

nullable를 계산하는 방법

X가 nullable이라면

1. empty string을 직접적으로 만들어낼 수 있는 경우 (x→e)
2. x→ YZ… production에서 RHS 심볼들이 다 nullable인 경우 (x→yz…)

알고리즘

모든 nonterminal은 Nullable이지 않다라고 가정한 후 rule을 하나씩 적용해서 변화가 없을 때까지 반복하면 된다.

first, follow를 찾는 방법

1) first 찾는 방법

• X가 터미널이면 x를 first에 추가
• 입실론이면 first에 e를 추가
• 여러개의 nontemrinal과 연결되어있고 first(yi)가 a라면 first(x)도 a가 되는데 단, 그 때는 y1~i-1까지 모두 입실론일 떄를 의미

ex) X-> y1 y2 y3 y4 있을 때 y1 first는 x의 first가 될 것

First(x) += first(y1), 하지만 y1이 입실론이 될 수 있다면 fist(y2)도 들어갈 수 있게 된다.

모두 y1….yk의 first에 입실론이 들어간다면 fist(x)에도 입실론이 들어간다 cf.

ex)

2) Follow 찾는 방법

• S가 start symbol이면 $를 추가(start뒤에는 더 나올 게 없으니까 end가 나와야 한다)
• follow(B) += first(beta) - e
• follow(B) += follow(A)

cf.

Putting it all Together

• 기본적으로는 first를 추가해준 후에 nullable한 nonterminal의 경우에는 follow도 추가해준다.
  • First 베타에 넣어주면 된다
  • 베타가 nullable이라면 followx에 넣어주면 된다

해당되지 않는 칸은 에러라고 볼 수 있다

cf. 문제는 이 문법은 LL1이냐? 아니라면 바꿔라 first, follow를 만들어라, 얘로 파싱할 수 있는 parsing table을 만들어라라고 나올 것

cf. 여기서 e는 입실론이 아니라 S’ → e에서의 →e를 의미하는 것!

Ambiguous Grammar

Topdown parser에서는 어떻게 나오는가?

테이블에 confilct이 생기게 된다, 즉, 같은 셀에 두개 이상의 production rule이 들어간다

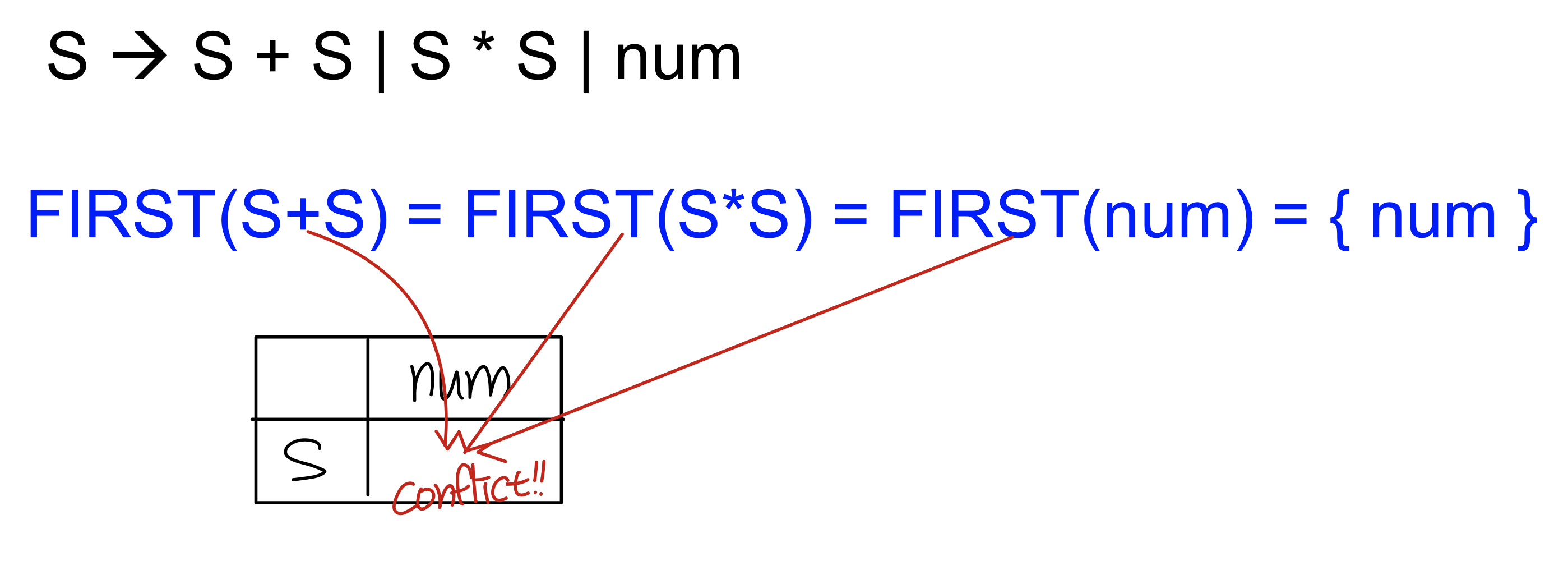
→ 그래머가 LL(1) grammar가 되도록 수정해주면 된다

creating the abstract syntax tree

call tree가 사실은 abstract syntax tree가 되는데 프로그램의 abstract syntax tree에 노드를 만들어서 연결해주면 됨

노드를 어떻게 만드는가를 배웠는데 AST 노드들을 어떻게 추가하는가?

left vs right associativity

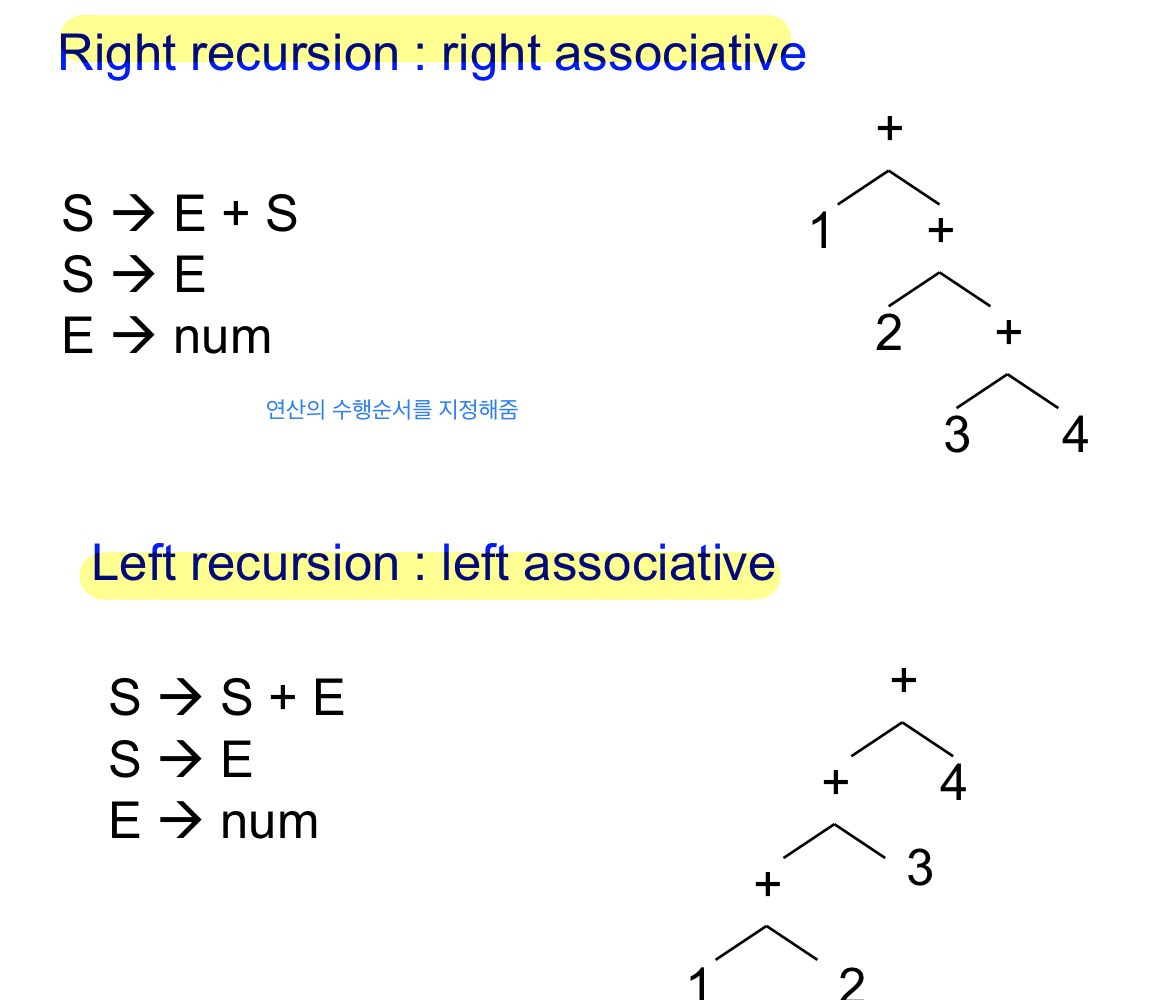
• left recursive grammar는 LL(1) grammar가 아니다
  • 언제 recursion을 끝내야 하는지 모르기 떄문에 top down parser에 사용할 수 없다

ex)

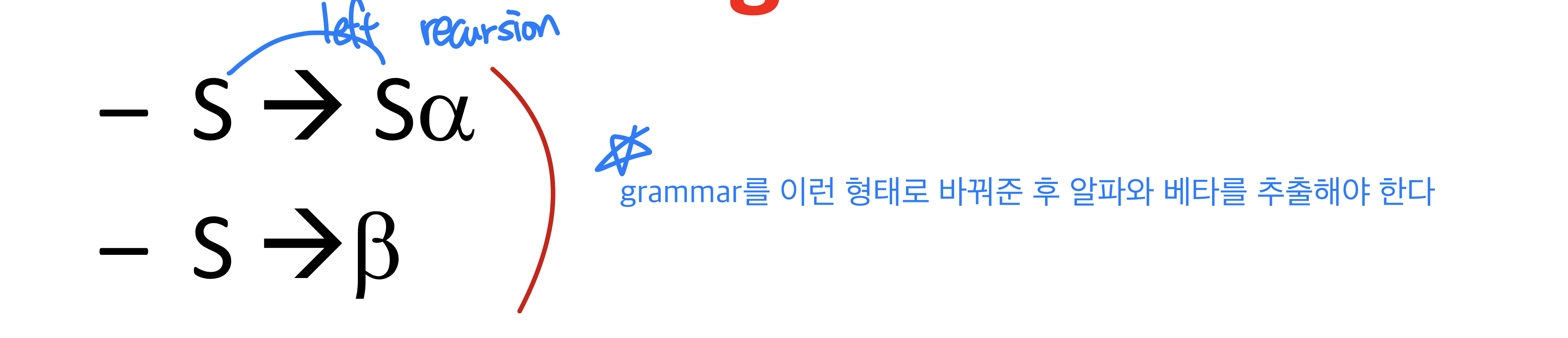
Left recursion elimination

cf.

어떻게 하는 건지는 알아놓을 것

(정리)

Top down Parsing Summary

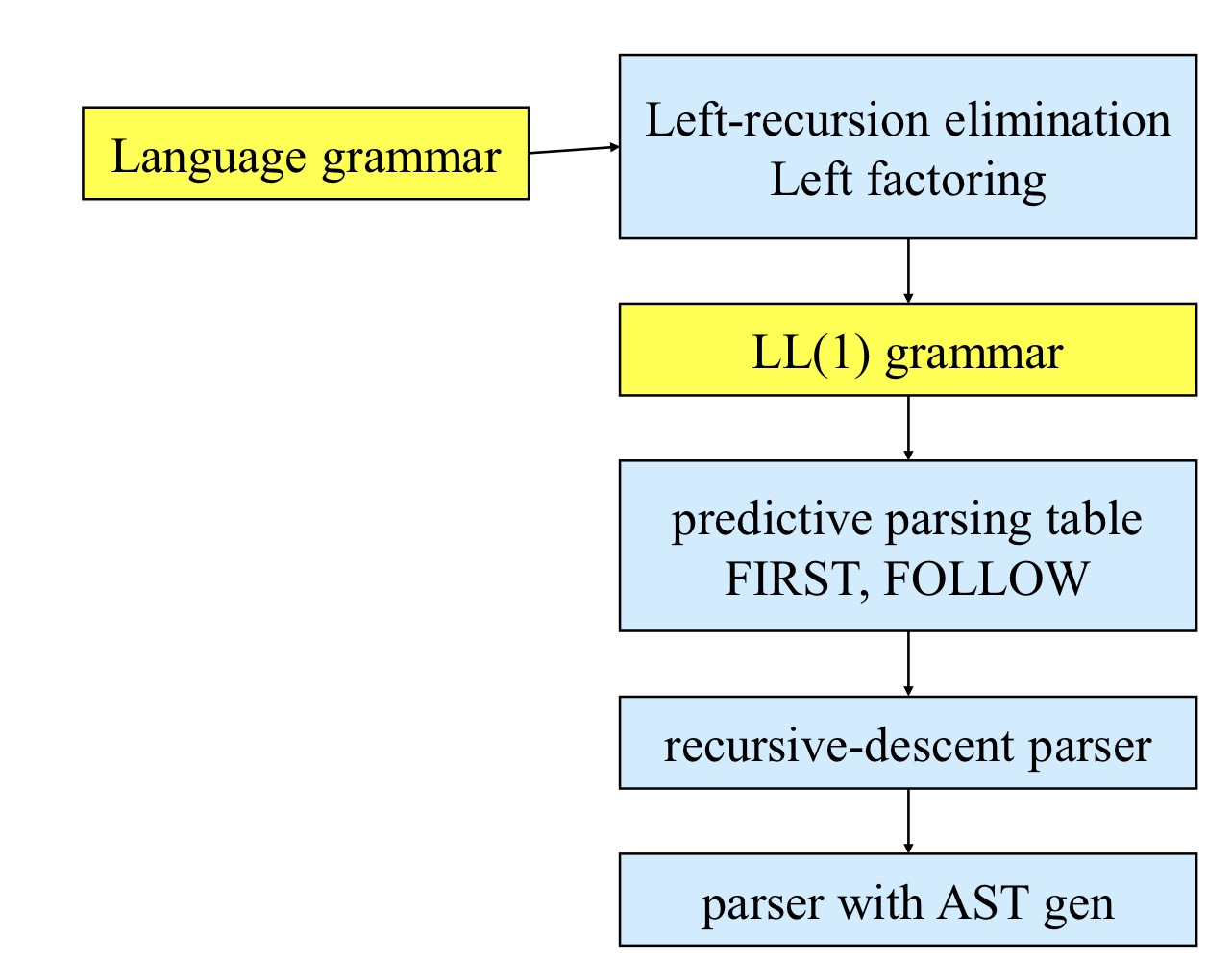
과정

Grammar-> ll1grammar로 만들기 -> first,follow 찾기 -> recursive-descent parser 만들기 -> parsing이 성공했다면 ast를 만들어야 한다 슬라이드 플로우를 따라서 이 예들을 잘 수행해보면 될 것

cf. First and follow는 right, left recursive 뭐든 적용 가능 만약 parsing table을 만들었을 때 같은 cell에 2개 이상의 production rule이 있다면 Grammar가 Ambiguous하거나 Ambiguous하지 않더라도 LL(1)이 아니거나 두 경우 모두 가능한 건가요?

• Ll1이 기본적으로 아니어서 문제가 되는데 LL(1)이 아니더라도 unambiguous할 수도 있음. 스펙을 unambiguous하게 정했다면 두개 이상이 들어갈 수 있음.기본적으로 같은 셀에 두개 이상 들어가면 LL(1)이 아니고 ambiguous 유무는 둘 다 가능할 것
• Lr이 너무 복잡해서 lalr이라는 걸 사실 더 많이 쓰임. 그래머가 Ambiguous하더라도 parser가 약간의 priority를 줘서 자기가 해결하는 테크닉도 있음 LL(1)은 빠름 – 과거를 다시 들춰보지 않으니까