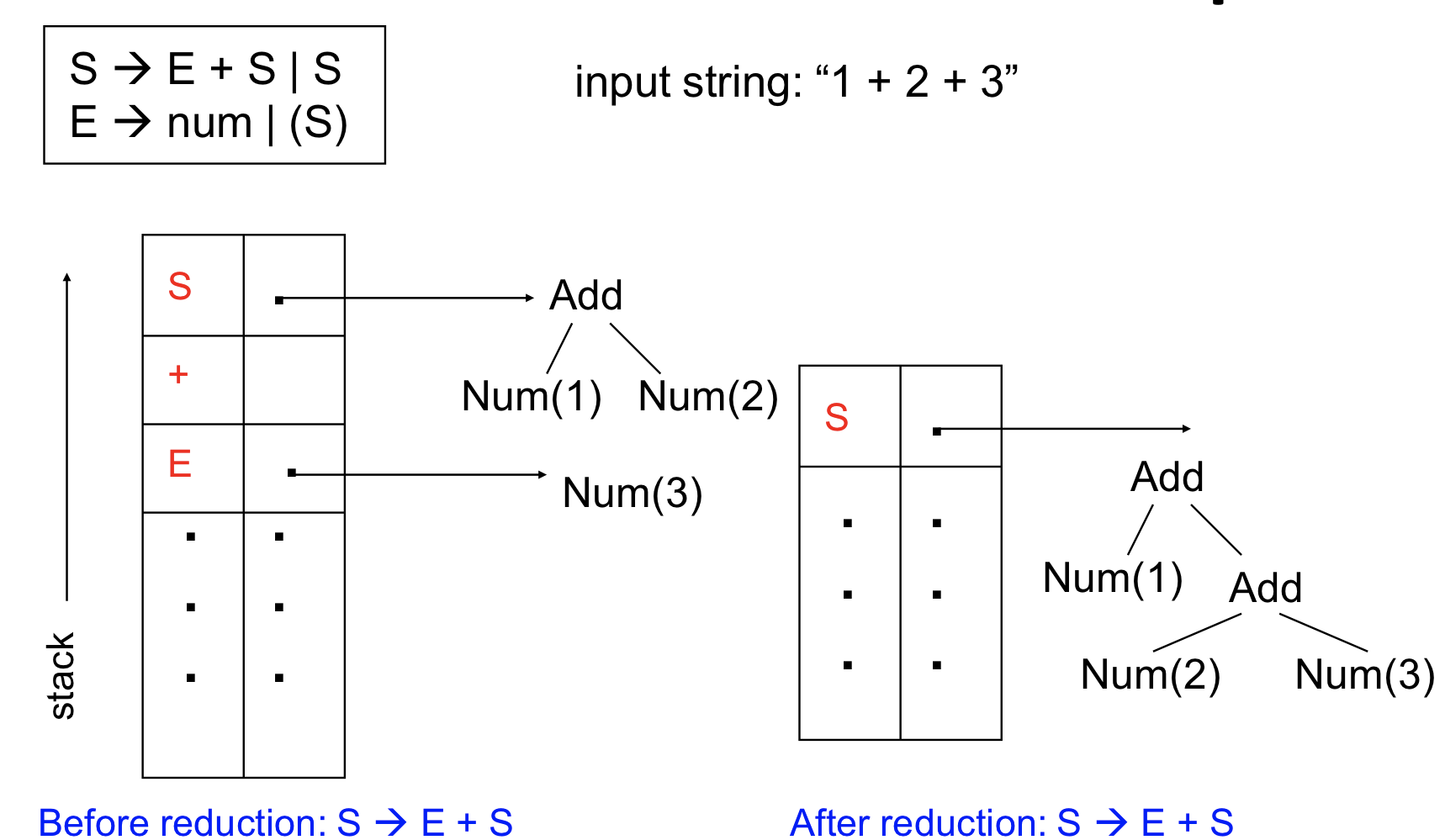
LR(0)는 스택과 lookahead를 사용해서 LL(1)보다 훨씬 powerful하지만 여전히 limitation이존재

• Lr(0)의 문제점을 보고 이걸 해결하기 위한 LR(1), SLR, LALR grammar에 대해서 알아보자
• lR(1)은 LR(0)에 limitation이 존재하고 LR(1)이 되면 limitation은 줄어들지만 state가 매누 많아진다.

→ 성능 대비 비용이 많이 들기 떄문에 state를 줄이는 것이 좋다.

• LALR은 LR1을 최적화한 것이고 SLR은 LR0에서 문제가 생길 때 조금 더 고려해서 해결하려고 하는 방법

LR(0) Limitations

• Lr(0) 머신은 lookahead 상관없이 언제나 state를 reduce를 할 수 있 때만 가능(single reduce action)
  • lookahead와 상관없이 reduce가 실행된다
• 하지만 복잡한 그래마일 경우 항상 shift/reduce conflict 나 reduce/reduce conflict 등의 문제가 생길

→ reduce일 때 허수인 값들이 존재하는데 이를 밝히는 방법은 s뒤에 follow가 있다면 혹은 내 뒤의 first를 찾을 수 있다면 그 안에 그 lookahead symbol이 없으면 된다.

1) shift-reduce conflict

어떠한 스테이트에서 lookahead가 있을 때 shift를 해야 하는지 reduce를 해야하는지  두개의 경우의 수가 있으므로 해결해야 한다

2) reduce-reduce conflict

룰을 거꾸로 적용할 수 있는 게 두개인 경우

→ Lookahead symbol을 무조건 봐야 한다

: 이때까지는 lookahead symbol을 보지 않고 reduce가 나오면 reduce를 실행했었는데 이제는 Lookahead symbol을 보고 shift/reduce라면 무엇을 할 건지 아니면 reduce 두 개 이상이라면 그 중 멀 할건지를 판단하자!

Non LR(0) grammar

I) left associative version

ii) right associative version

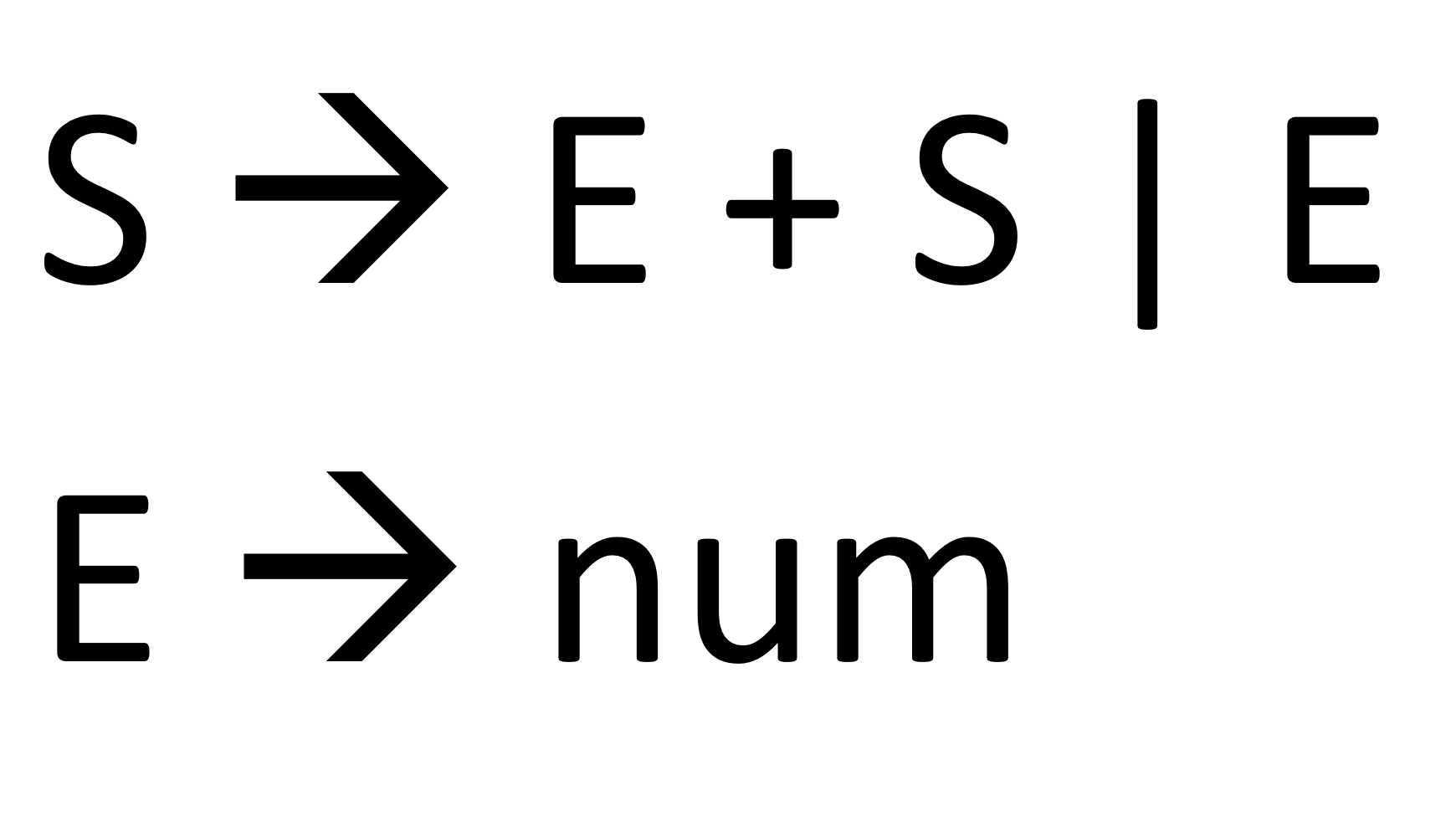
• Left associative 버전은 LR(0)인데 right associative는 LR(0)가 아니다

→ Lr(1)을 사용해서 풀어야 한다

• Right associative grammar는 LR(0)이 아니며 Top-down parsing(LL(1) parsing)에서는 수행 가능. shift reduce state를 만들기 위해서 굳이 right associative grammar를 사용할 경우 겹치는 부분이 생긴다
  • LL(1) grammar는 기본적으로 Right associative grammar가 좋다.
  • left associative는 LR(0)일 가능성이 크다

Q. C 프로그램은 left associative한 걸로만으로 만들 수 있을까?? A. 없다. 왜냐면 대부분 왼쪽부터 하지만 오른쪽부터 하는 게 존재 :지수(2^3) Lr(0) grammar는 left associative만 되고 right associative는 안됨 근데 상용 parser는 right associative도 support하기 위해 conflict를 해결한다

• 기본적으로 lr(0)에서 conflict이 일어나는 것은 right associative이기 때문

right associate LR(0) grammar의 parsing table

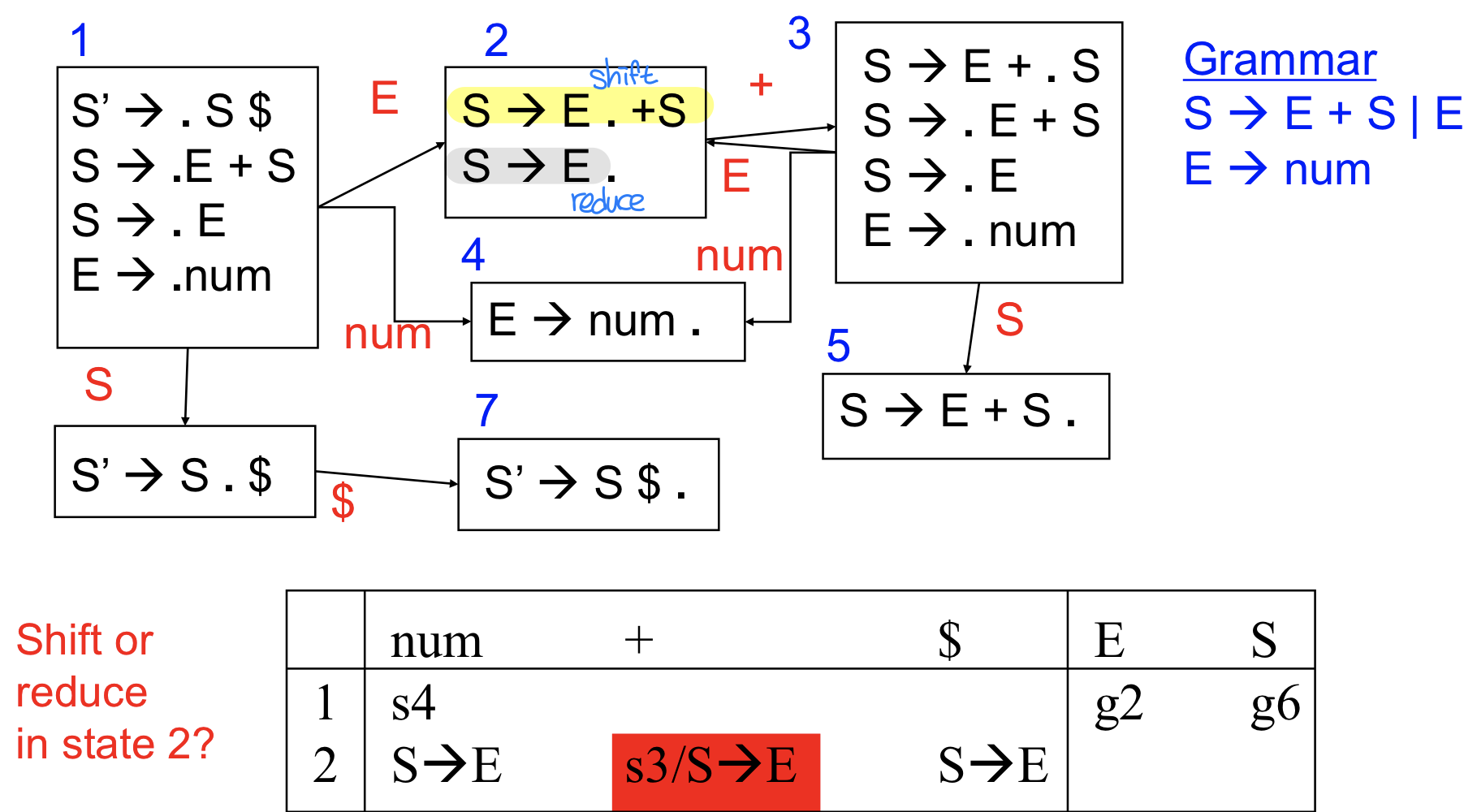
이때 대부분의 경우는 left associative와 비슷하지만 state 2를 보면 두가지가 가능하게 되는데 위는 shift, 밑은 reduce를 수행해야 한다.

즉, 파싱 테이블로 선택 시 reduce할 지 shift를 할지 결정할 수 없게 된다.

→ Lookahead로 해결해보자! 스택의 맨 위에 2번 state이며 그 때 lookahead가 s의 follow에 들어있는 심볼일 경우에만 reduce를 해야 한다. S의 follow에 +가 없다면 shift를 해야 한다.

뒤에 나올 수 있다면 reduce를 해야하고 뒤에 나올 수 없다면 reduce할 때 그 토큰은 나올 수 없다!

즉, S의 follow에 나올 수 있는 terminal만 reduce를 하도록 한다

Solve Conflict with Lookahead

하나의 lookahead를 추가해서 충돌을 해결하는 세가지 방법이 존재

• SLR : simple LR
• LALR : lookahead LR
• LR(1)

-Lr(1)이 가장 커버리지가 높고 일반적인 방법이지만 State가 엄청 늘어난다는 단점이 있어 slr, lalr이 쓰이며 그 중에서도 LALR이 많이 쓰이는 편(SLR<LALR< LR(1),웬만하면 SLR에서 끝나는 것이 좋다)

SLR Parsing

• Easy extension of LR(0) : Lr(0)를 기반으로 conflict를 제거

cf. LR(0)는 일단 lookahead를 보지 않기 때문에 reduce일 경우 lookahead가 무엇인지 항상 시행하게 된다는 단점이 존재, Reduce action이 수행되는 state의 경우에서는 모든 lookahead symbol에 대하여 reduce action이 인가된다

→ 언제 reduction을 수행해야 하는가를 보고 LR parsing table을 간단하게 만들어주는 기법

• reduction X → b, 수행시 lookahead symbol은 C라고 하면, C가 follow(X)에 들어 있을 경우에만 reduction을 수행

  x->b에서 x가 나오게 될 텐데 x뒤에 무조건 c가 나올 수 있다면 스택에 맨 위에 베타가 있다면 아 이게 x에서 유래된 b이구나 판단 가능! 근데 follow에 c가 없다면 top에 있는 값이 실제로는 b라고 생각했지만 b가 아니게 된다

  → reduction하는 경우의 수를 줄일 수 있다

• 모든 충돌을 제거해주지는 못하고 some conflict를 제거해준다.
• LR(0) table과 reduction row를 제외하고 모두 동일하지만 reduction은 Follow(x)에 들어있는 심볼 column에만 x→b를 추가해준다.

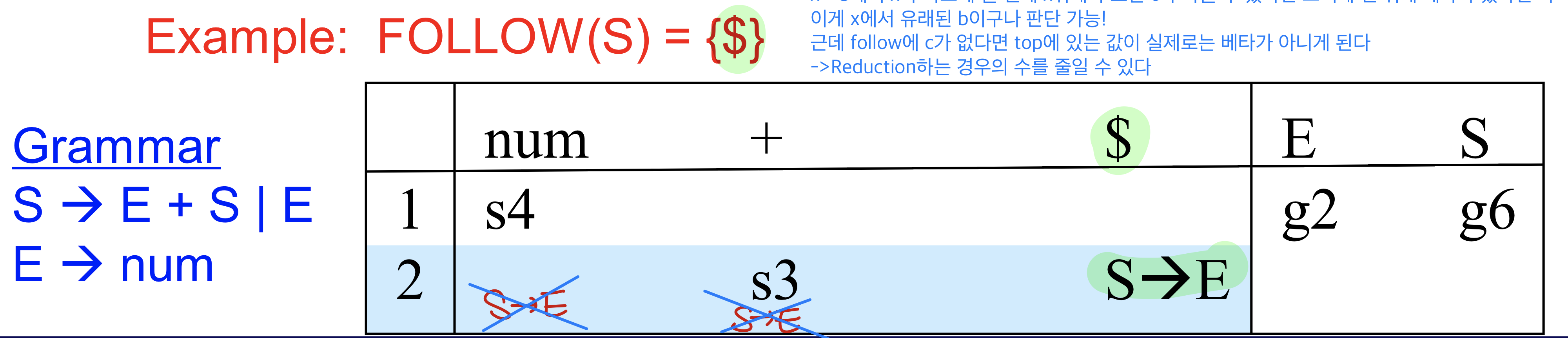
cf. 만약에 S의 follow에 +가 들어있는 경우라면?? SLR로는 해결 불가!

SLR parsing Table

• reduction이 row에 모두 들어가지 않는다는 것을 제외하고는 나머지는 LR(0)과 동일

→ Lr parsing table보다 간단한 편

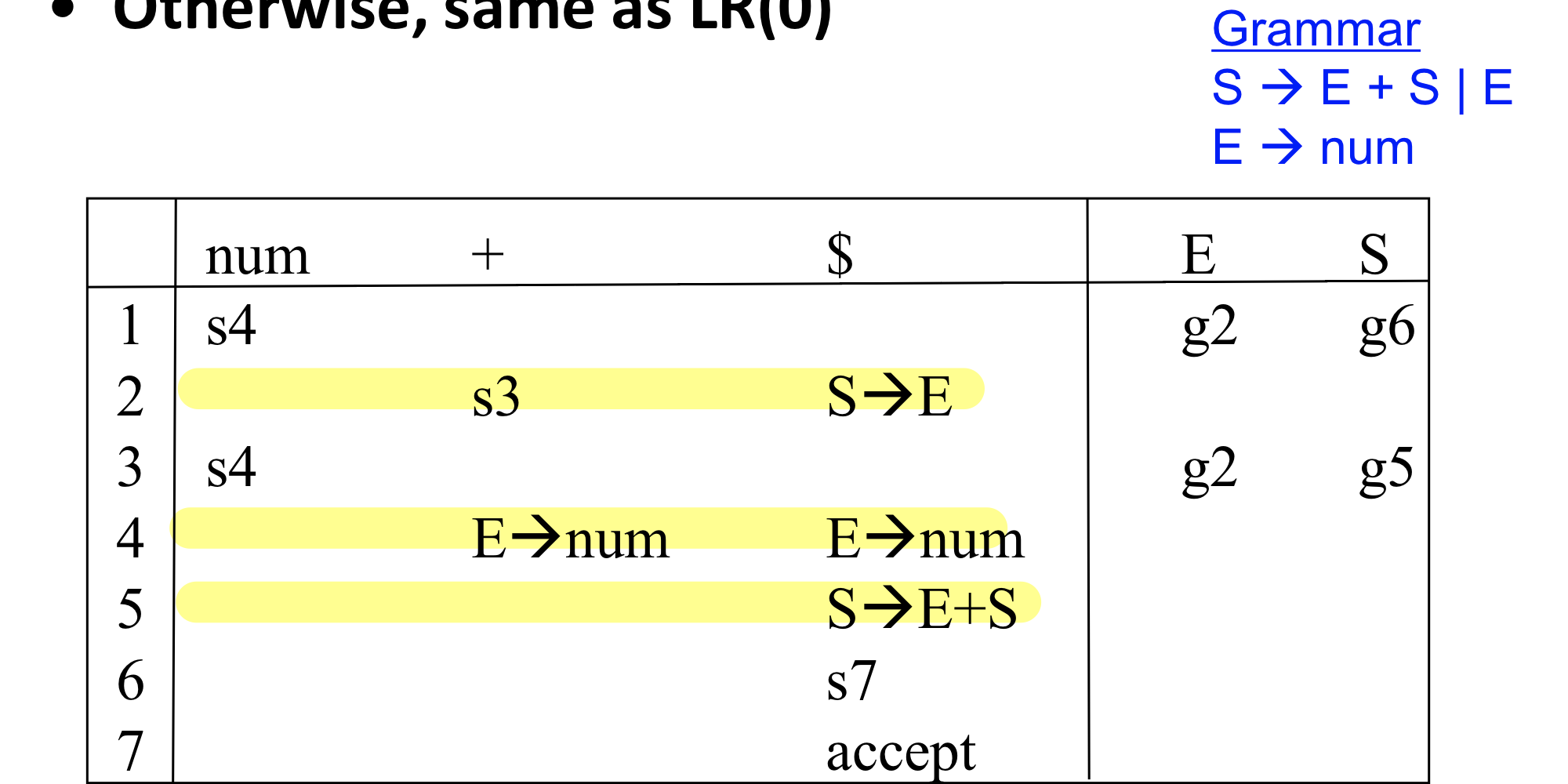
• 원래 shift는 하나의 terminal, lookahead에 의존했는데 reduce도 하나의 lookahead에 의존하여 follow로 허수들을 지워줌으로써 더 명료해졌다.
• 하지만 Slr도 완벽하게 충돌을 없애 주지는 못한다. Slr은 reduce가 가능한 경우만 표시하여 대부분의 reduce-reduce conflict을 해결해 주지만 reduce-reduce conflict을 막아주지는 못하므로 근본적인 해결방법인 lr(1) parsing에 대해서 알아보자!

cf. 해당 그래머가 LL(1)인지 확인하려면 parsing table을 만들어야 하지만 conflict이 일어날만한 상황이 직관적으로 보인다면 그 부분만 확인해도 상관 x

LR(1) Parsing

• 하나의 lookahead symbol를 항상 살펴보는 파싱 테이블
• LR(1) grammar = recognizable by a shift/reduce parser with 1 lookahead

Lr(0)에서 필요한 state는 Lookahead를 고려하지 않았지만 이제는 고려할 것

• Lr0와 비슷하게 parser state(stack과 lookahead symbol을 기반으로 parser를 만들어준다
  • parser state(현재 스테이트의 역사를 대변해주는 상태를 의미) : item의 모임
  • LR(1) item : lr 0 item + lookahead symbol possibly following production

  

• lookahead symbol은 프로덕션뒤에 존재할 수 있는 가능한 lookahead symbol에 대한 정보를 추가해주는 것으로 reduce에서만 영향이 있다. shift에서는 사용하지 않는다.

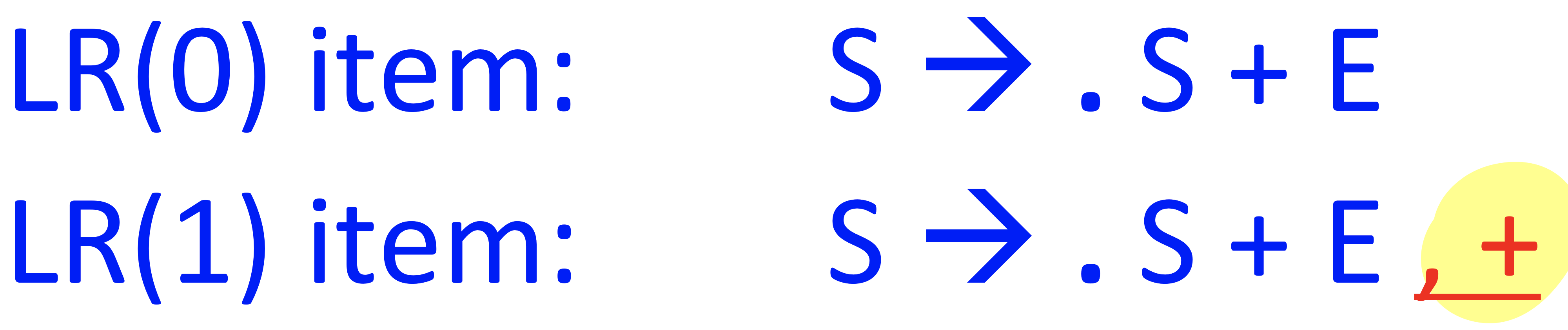
Lr0 item : .로 현재의 progress를 포인트로 지정

Lr1 item : 현재의 progress + 이 production 뒤에 존재할 수 있는 lookahead symbol을 추가

LR(1) states

LR(1) state

set of LR(1) items

LR(1) item = (X→ a.b, y)

의미 : a는 이미 tos에 매치되며 그다음에 by를 보기 희망한다

Q. y가 중요한 경우는 언제?

A. b가 null인 경우 y를 고려한다. b가 null이라면 뒤에 머가 나오는지 봐야 한다.

• shorthand notation

  

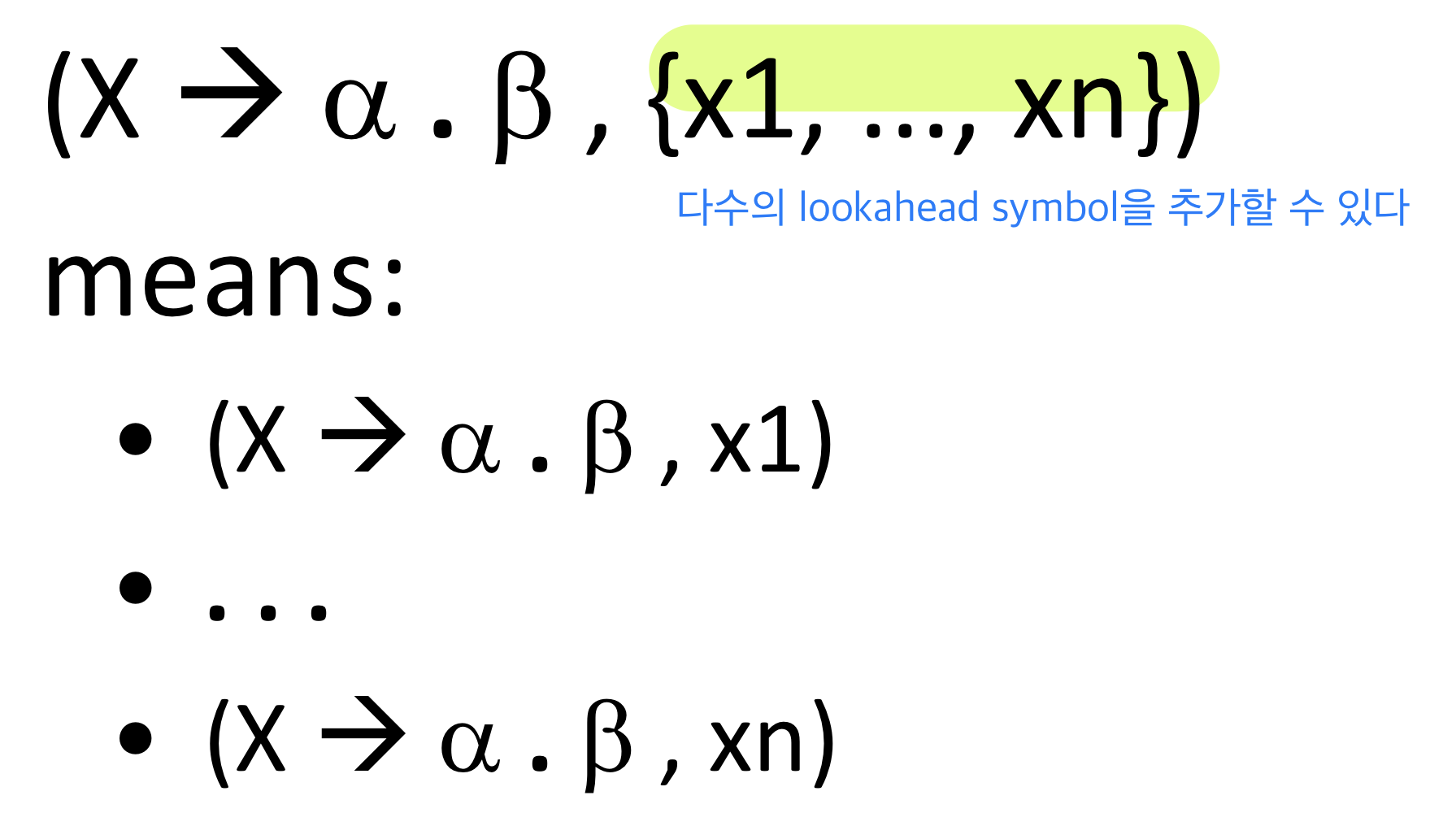
• 다수의 lookahead symbol을 추가할 수 있다
• Closure과 goto operations도 역시나 lookahead symbol을 추가할 수 있어야 한다

cf. Associativity로 conflict이 나올 수 있는데 bison은 조금 잘못되거나 정보를 다 주지 않았을 때도 알아서 해결해야 하므로 lr parser에서 conflict이 있을 때 자체적으로 멀 먼저 선택해야하는지 해야한다. Shift reduce가 있을 때 멀 먼저 수행할건지 reduce reduce가 있을 때에도 어떤 연산자가 좀 더 우선순위가 있는지를 살펴보면 약간 grammar가 ambiguous해도 해결할 수 있게 된다. → Left associative는 reduce, right는 shift를 한다. reduce가 두 개가 있다면 여기서 멀 먼저해야하는가는 우선순위로 결정할 수도 있음

LR(1) Closure

LR(1) closure operation

S에서 시행해서 .뒤에 가능한 production rule이 있다면 추가, 새로운 production rule을 추가하고 y뒤에 나올 수 있는 first가 중요하기에 first(bz)를 구함

• LR(0) closure와 비슷하지만 lookahead symbol을 저장해야 한다

LR(1) Start state

• initial state = (S’ -> .s, $)

cf. LR(0)에서의 initial state는 S’→ .S$

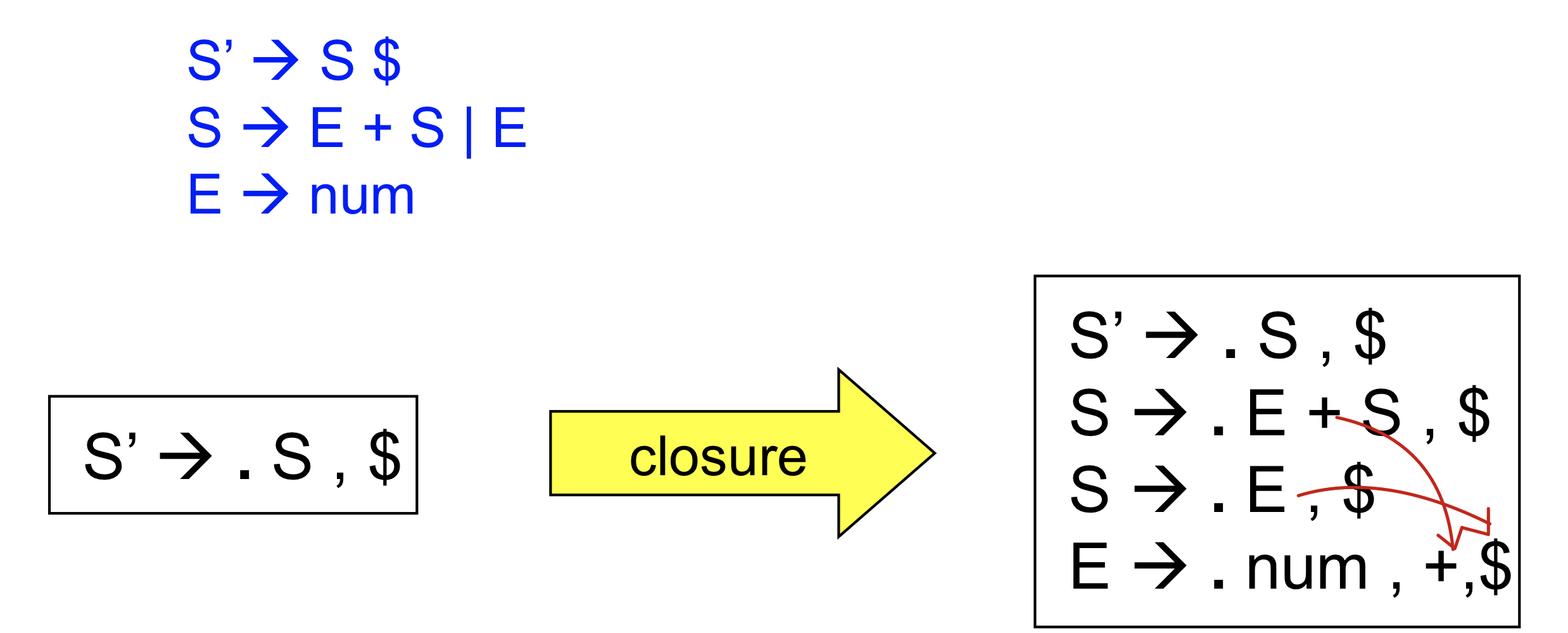
마지막에 +가 추가되는 이유는 e+s에서 +가 뒤에 올 수 있기 떄문, 그리고 e 뒤에는 달러도 올 수 있기 때문

LR(1) Goto Operation

• LR(1) state 사이에서의 transition하는 operation을 의미

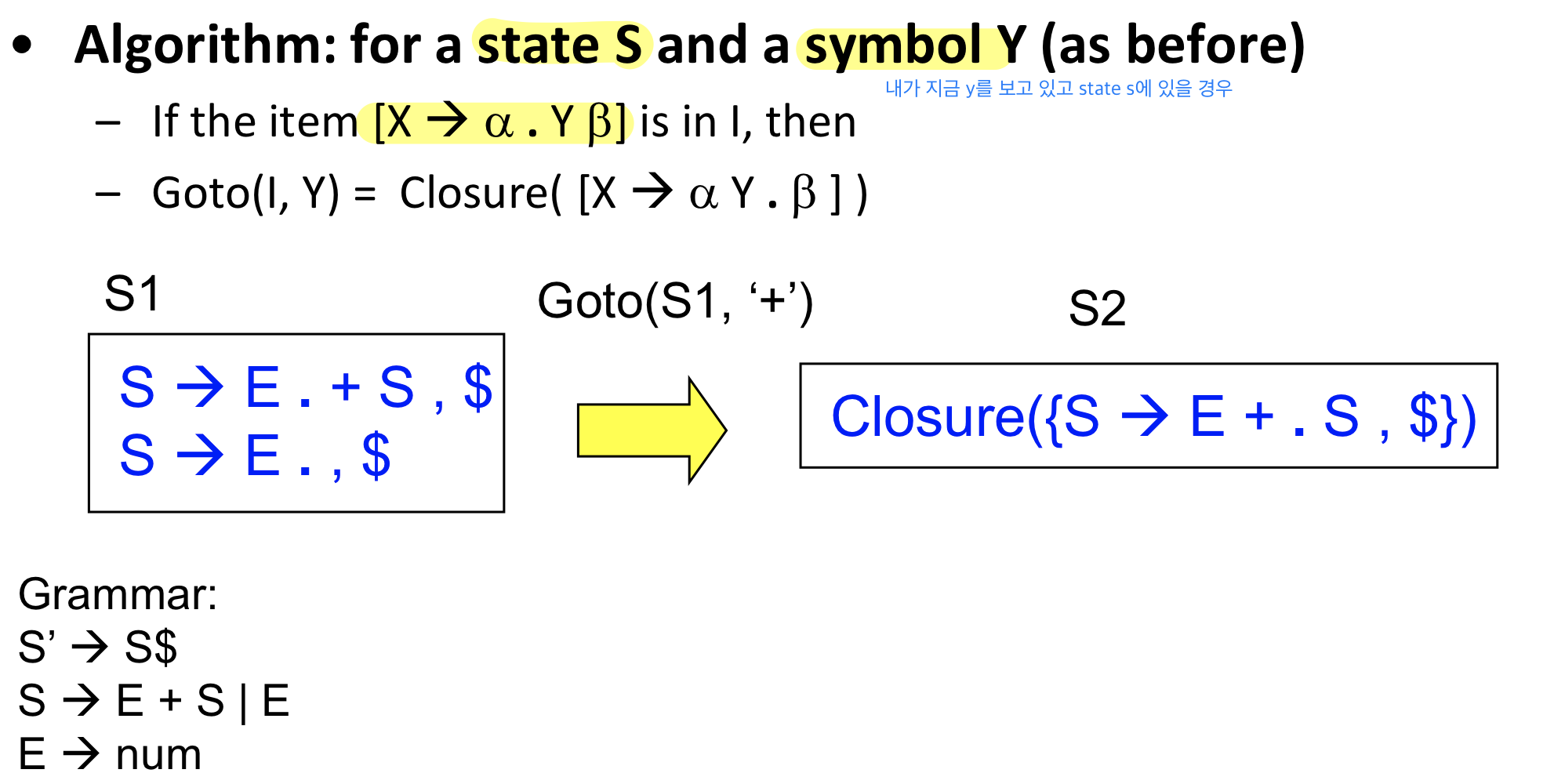
LR(1) DFA Construction

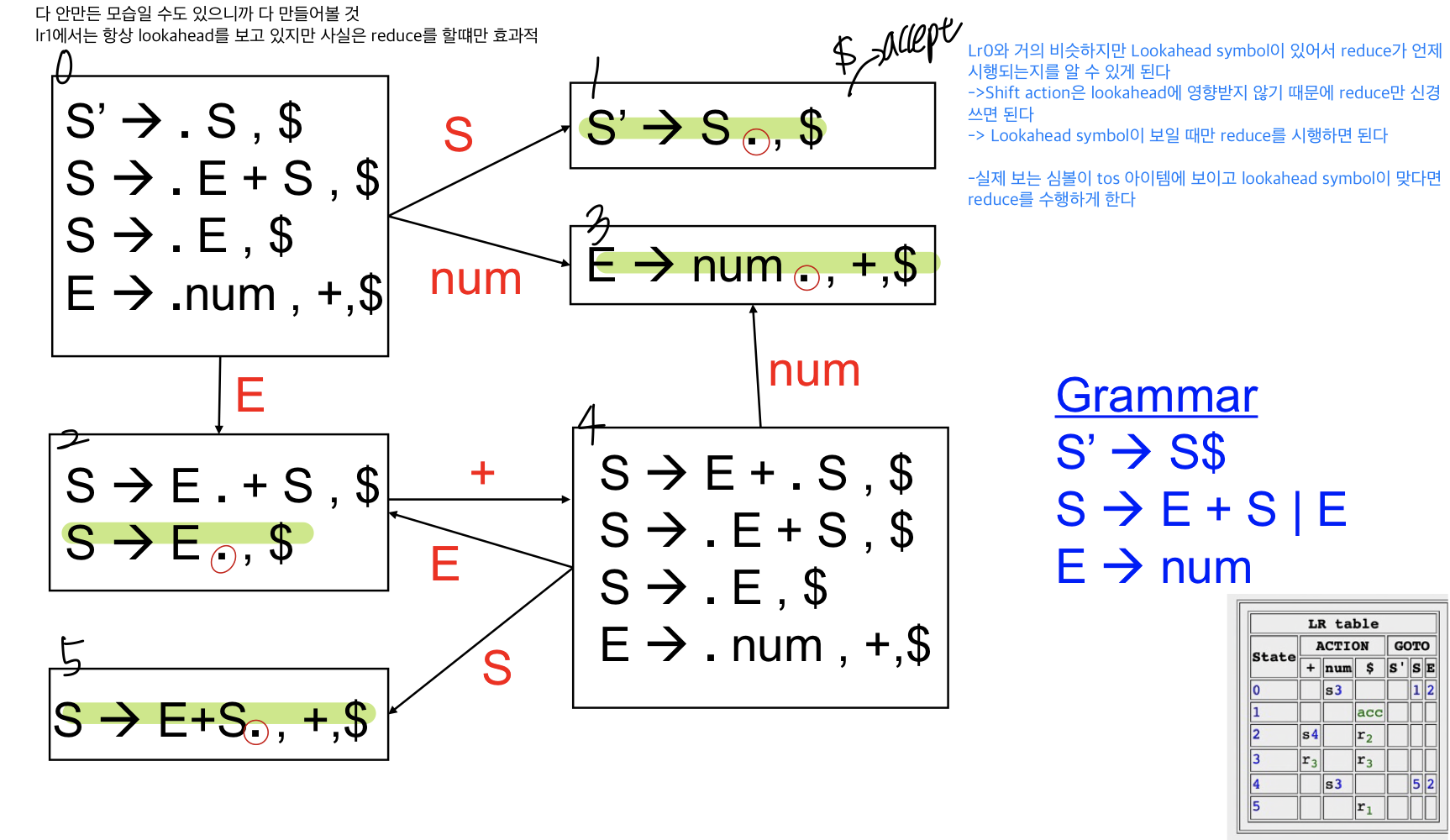
LR(0)와 거의 비슷하지만 Lookahead symbol이 있어서 reduce가 언제 시행되는지를 알 수 있게 된다

• Shift action은 lookahead에 영향받지 않기 때문에 reduce만 신경쓰면 된다

→ Lookahead symbol이 보일 때만 reduce를 시행하면 된다

• 실제 보는 심볼이 tos 아이템에 보이고 lookahead symbol이 맞다면 reduce를 수행하게 한다(X→r. ,y)

• reduce는 .이 가장 마지막에 있는 state에서 lookahead symbol column에 추가하면 된다.

  단 여기서 S’→S. , $는 accept으로 끝나는 state이므로 reduce하지 않는다.

LR(1) Parsing Table Construction

• 기본적으로 lr0과는 동일하지만 reduce만 다름

S→S’ on terminal X

• Terminal을 보면 밖에서 토큰을 받아오는 거니까 shift 수행
• Table[S,x] += Shift(S’)

S→S’ on non-terminal N

• Nonterminal을 보게 되면 reduce가 일어나서 새로운 nonterminal이 나온 것 이므로 goto를 실행
• Table[S,N] += Goto(S’)

I contain {(X→ r.,y)} :

• Table[I,y] += Reduce(X→r)
• r.이고 y를 볼 때에는 reduce를 하면 된다

ex) parsing table example

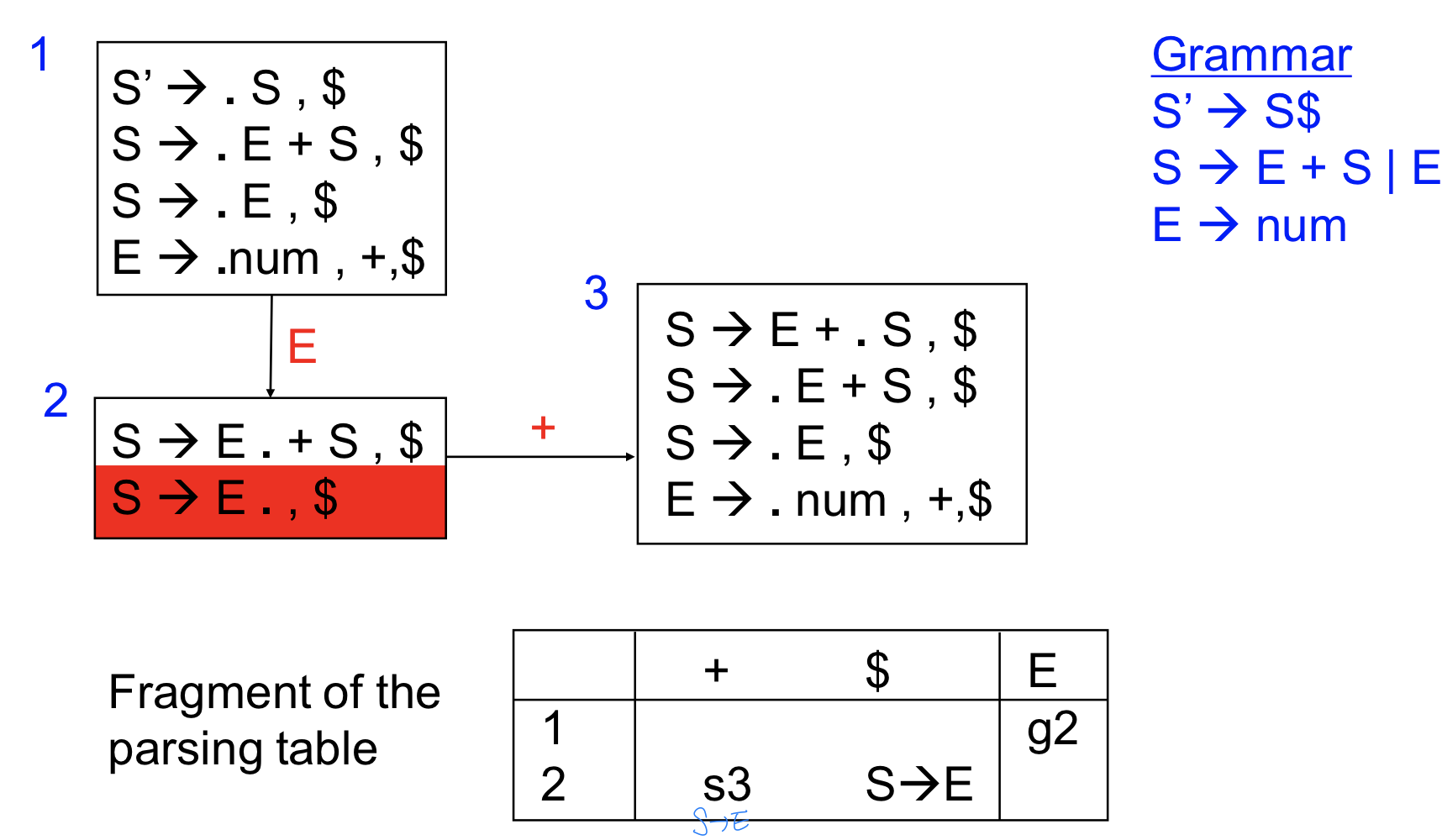
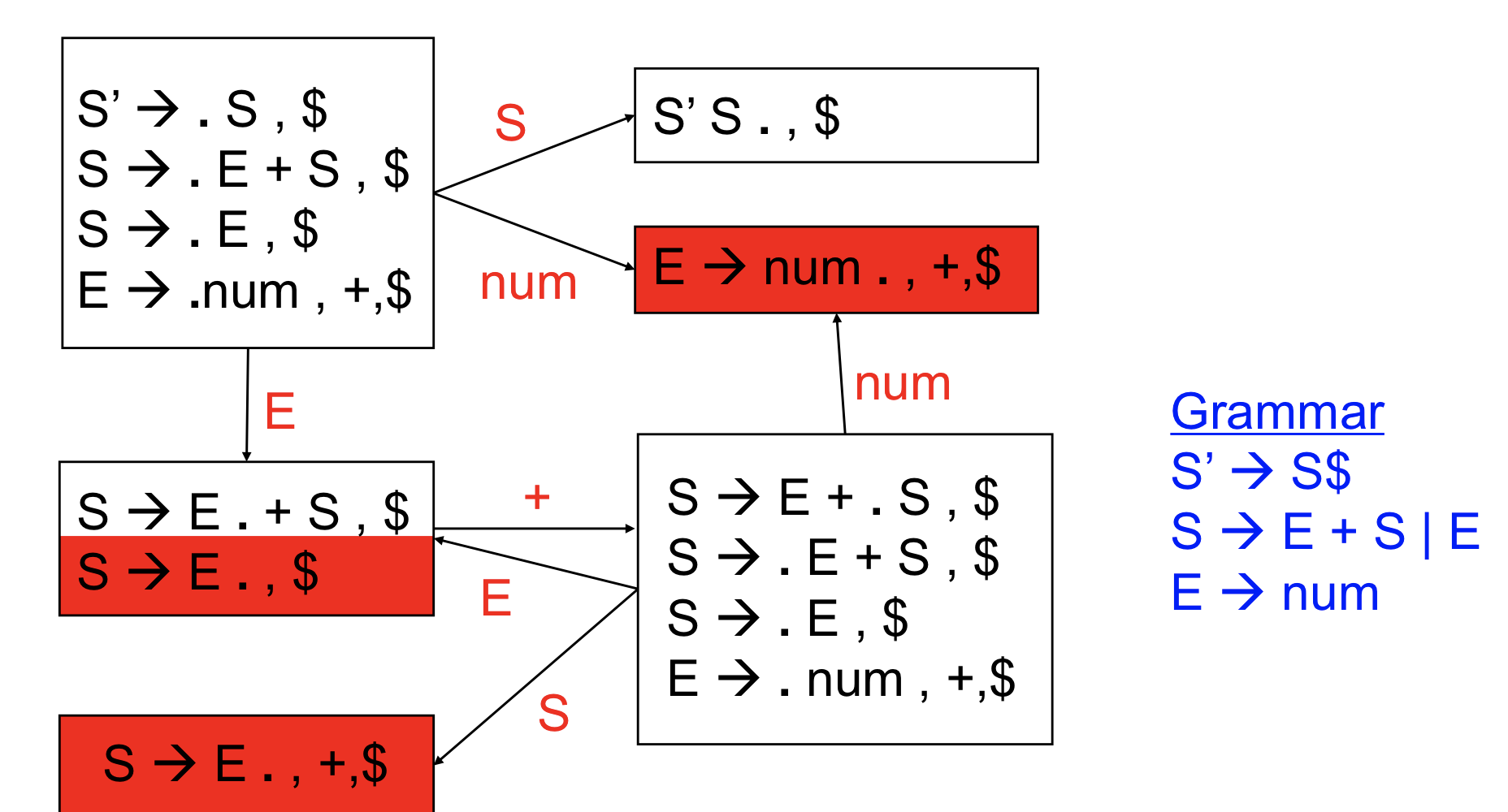
LR(0)에서는 conflict임 : s->e가 모든 lookahead에서 reduce에서 일어나야 하기 때문에 conflict이 일어날 것, lr1에서는 specific하게 지정하기 때문에 +가 lookahead일 경우에는 reduction을 수행하지 않아도 된다.

• +일 때에는 shift, $일 때는 reduce를 하면 된다

  cf. S→ E.+S, S S→ E. +,$

  인 경우에는 conflict이 일어날 수 있다! 여기서는 LR(1) grammar가 아니라는 의미이며 right associative grammar일 때 이런 문제가 생길 수 있다.

LALR(1) Grammars(LookAhead LR)

• LR(1)의 문제점

Lr 1 은 커버리지가 높지만 state가 너무 많이 나오는 것이 문제, 이전까지는 progress만 보면 되었지만 이젠 lookahead도 봐야 하니까 너무 많이 나오는 스테이트들을 줄여줄 수 있는 방법!

→ 중복되는 state들을 합치자!!

• Lr(1)을 만든 뒤에 어떤 두개의 state가 item들이 다 같고 lookahead만 다를 경우 합친다(approximate)

→ 더 사이즈가 작은 parser table을 만들 수 있지만 LR(1)보다는 덜 powerful하다.

• State 수를 줄인다면 파싱 테이블의 사이즈를 줄일 수 있다-> 메모리를 효율적으로 사용하는 것이 중요하기 때문!! 속도와도 연관이 있기 때문
• Lookahead symbol이 다르고 production rule이 같다면 합치기에 오류가 생길 수 있기는 하지만 현실적으로는 겹치는 경우가 많지 않아 주로 많이 사용
• 대부분의 경우에는 문제가 없지만 엄밀하게 하다면 문제가 생길 수는 있으나 대부분 문제가 되지 않아서 사용

⇒ LALR(1) : LALR(1) parsing table에 conflict이 없는 경우

LALR Parser

• SLR와 거의 비슷하게 state 수가 나오게 된다(LR(1)보다는 훨씬 작은 값)
• 하지만 SLR 보다는 훨씬 좋은 lookahead capability를 가져 reduce/reduce conflict이 보통 해결된다
• Lalr이 가장 많이 사용됨
• SLR보다는 성능이 좋고 LR(1)보다는 state가 적으며 성능이 조금 떨어짐.

LL/LR Grammar Summary

• LL parsing tables(top down parser)

Non-terminal X terminal → Productions

nonterminal과 terminal로 Production을 어떻게 할 것인지 first와 follow로 계산한다

• LR parsing tables(Bottom up parser)

LR states X terminal → {Shift/reduce}

LR states X non-terminal → goto

dfa simulation을 사용해서 state transition rule을 만들고 stack과 lookahead symbol을 이용해서 closure/goto operation을 계산하여 parsing table을 만든다. State와 terminal을 가지고 shift할지 reduce를 할지 판단

-State와 nonterminal은 reduce 수행 후에 스테이트를 업데이트하기 위한 테이블

-두개의 테이블이지만 하나로 합쳐서 사용

Classification of Grammars

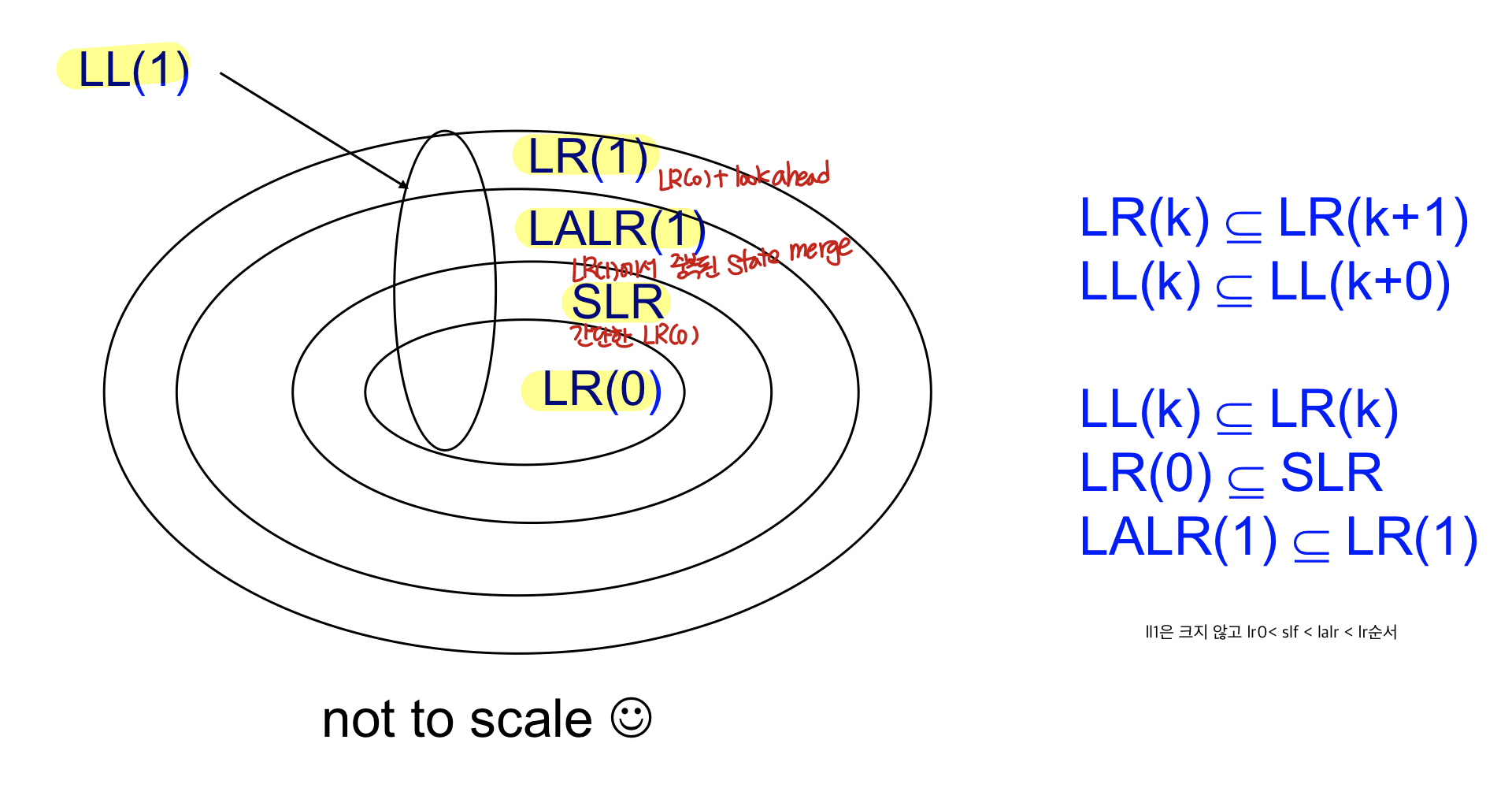
보통 커버리지를 나타내는데 ll1은 크지 않은 편

점점 커지는 경향(LR(0) < SLR < LALR(1) < LR(1))

Q. 어떠한 그래머가 있을 때 lr1 grammar인지 테스트하라고 했을 때 이게 left factoring을 하거나 left associative elimination을 수행하면 ll1이 되지 않나?? A. 근데 factoring이나 elimination을 해서 ll1이 되냐가 아니라 지금 있는거에서 문제가 생기면 ll1이 아닌 것 얘를 어떠한 걸 취하면 ll1이 되는 가? Factoring, elimination이 필요하면 lr1이 아닌거!!실수하지 말고 잘 알고 있을 것

Automate the Parsing Process

• LR table을 만들고 그것을 바탕으로 shift-reduce parser를 만드는 것을 자동화해야 해야 한다

LALR(1) parer generators

• lr parsing table을 자동으로 만들어줄 수 있는 yacc, bison
• LR1과 거의 다르지 않지만 LR1보다는 parsing table의 사이즈가 작다.
• augment LALR(1) grammar specification with declarations of precedence, associativity
• output : LALR(1) parser program

Associativity

lalr parser의 문법이 애매한 경우)

LR(1)을 사용하다고 하더라도 conflict가 생길 수 있는데 이때는 CFG자체에 문제가 있는 경우이다

하지만 마음대로 CFG를 바꿀 수는 없는 경우도 존재

→ bison은 이러한 conflict을 해결하기 위해 어떻게 해결하는가?

왼쪽은 left associative인데 얘를 오른쪽으로 바꾸게 된다면 애매하게 된다

LR(1)으로 만들었어도 무넺가 생긴다. lookahead가 reduce 시 + 이므로 shift도 +에서 시행되므로 문제가 생김

→ LALR(1)을 만들게 되면 원하는 associativity를 지정할 수 있다

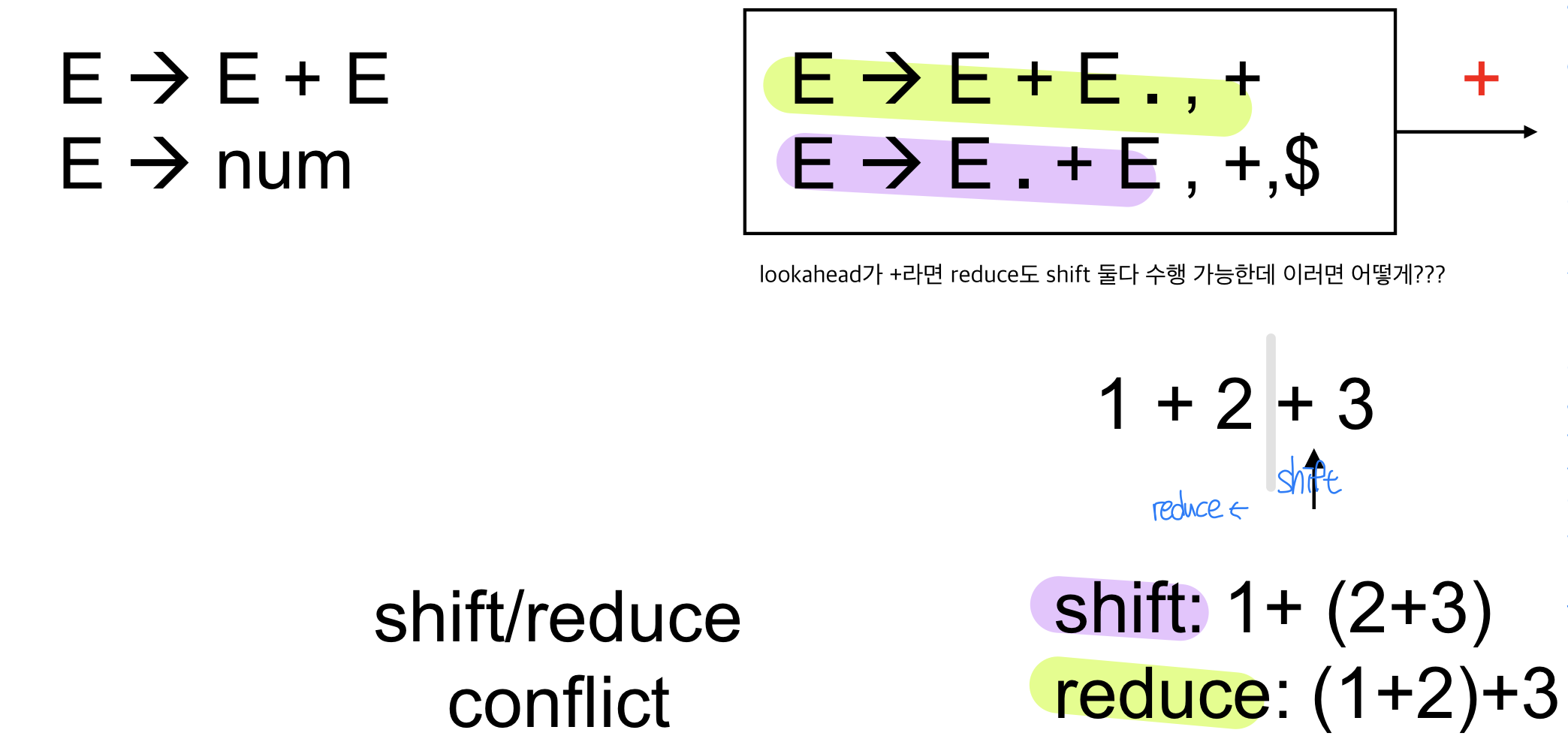
여기서 lookahead가 +이면 문제가 생기게 됨 shift도 가능하며 reduce도 가능하게 된다

• 이러한 경우에도 조정을 통해서 associativity가 가능
• 1+2까지 들어있다면 1+2로 reduce할수도 있고 +를 shift할수도 있음

i) shift를 했다면 +를 추가한 것이기 떄문에 2+3을 먼저 계산하게 된다

ii) Reduce를 했다면 1+2를 먼저 하게 되는 것

→ Shift/reduce conflict에서 shift했다는 것은 right associative한 것이고 reduce는 left associative한 것 !즉, shift를 하면 나중에 들어온 아이 먼저 해결되고 reduce는 왼쪽부터 계산하게 됨

⇒ 우리가 우선성을 만들어주면 애매한 문법도 해결할 수 있게 된다.

left associtve -> reduce에 좀 더 우선순위(common sense에 부합)

• 토큰으로 보는 것보다 스택에 있는 것에 우선권을 더 준다는 의미

right  associative -> shift에 좀 더 우선순위

• stack에 있는 것보다 lookahead가 더 우선순위가 높을 경우

Precedence

이것도 사실 왼쪽은 문제없지만 오른쪽처럼 만들면 애매해진다( +,*의 우선순위가 없기 때문)

→ priority를 줄 수 있다

• 왼쪽 그림의 경우 - 위는 shift, 밑은 reduce인데 + 보다는 *가 먼저 계산되어야 하니까(input token이 +인데 스택에 있는게 *이므로 Input token이 더 낮으니까) reduce를 먼저 하도록 하게 한다.
• 오른쪽 그림의 경우 - 위는 reduce, 밑은 shift인데 *가 먼저 계산되어야 하므로 shift를 먼저 하도록 한다.

Input toke stream > 스택의 마지막 터미널 : shift

Input token stream < Stack의 마지막 terminal : reduce

Abstract Syntax Tree(AST)

derivation

• sequence of applied productions

Parse tree

• derivaiton을 그래프로 표현

AST

• parse tree에서 불필요한 정보를 제거

Implicit AST construction

• LL parsing : AST는 production으로 표현

• LR parsing : AST는 reduction으로 표현
  • ASTconstructionmechanism – Store parts of the tree on the stack – For each nonterminal symbol X on stack, also store the sub-tree rooted at X on stack – Whenever the parser performs a reduce operation for a production X→ r, create an AST node for X