Type checking과 scope에 대해서 배웠는데 static semantic에서 알아보자!

Static Semantics

: 프로그램에서 이용되는 타입을 표현하는 언어

  • 원하는 타입을 어떻게 type check할 것인지 기술

  • 프로그래밍 언어에서 type checking을 위해서 이용하는 formal description이라고 볼 수 있다

    Syntax – context free grammar

    Lex – regular expression 와 같다고 보면 된다

  • Programming language(legal AST)에서 타입들을 define한다고 생각하면 된다

Type judegment or relation

Static semantics

타입을 판단하는 방법에 대해서 formal하게 표현함

E : T

  • 어떠한 expression이 있고 이게 t란 타입으로 정의됨을 알려주는 식을 사용
  • 이 expression은 type t로 잘 타입이 정의된 expression이다

이러한 구문이 있다면 t라는 타입으로 호환됨을 의미

Ex) type judgment

Untitled

2는 int 타입으로 well-typed되어있다. Expression을 다 수행하면 integer와 호환된다

Type judgments for Statements

구문에 대한 type judgment에 대해서 알아보자

  • 구문은 수식이 될 수도 있기에 비슷함
  • use type judgments for statements

Untitled

  • Statement가 수식이 아니라면 아무것도 타입을 만들지 않는 경우에는 unit type 지정 가능

    S : unit

    아무런 수식의 결과가 없고 내용이 없다면 unit type이라고 지정한다

    →구문 s는 어떠한 result type으로도 well type되지 않는다

Deriving a Judgment

Judgement를 도출해보자

  • 구문에 대한 judgement가 진짜인지 아닌지 판단해야 한다
  • 어떠한 조건에서 true인지 판단할 수 있어야 한다. 이러한 판단이 실제로 도출되는지 알아봐야 한다

도출하는 과정 – deriving a judgement

ex) If (b) 2 else 3 : int

Q. 이 때 구문이 integer type으로 well typed이 되려면 어떤 조건이 필요한가?

A.

Untitled

B가 bool이 되어야하고 2가 int, 3이 intd여야 이 구문이 integer로 well type 임을 알 수 있다

Type judgements

A : 문맥, context

  • Type judgement notation : **A - E : T**

    어떠한 문맥 a에서 expression e는 type T로 well typed expression이다

  • A는 문맥이므로 현재 상황에서 알 수 있는 정보가 a에 들어간다 이게 type context!
  • type context는 지금까지 우리가 알고 있는 type binding의 set를 의미한다. Id가 T로 binding되어 있다 type binding 정보는 사실 symbol table안에 들어 있음

Untitled

현재 b,x가 type context에 들어가 있을 때 B는 bool이 참이다. B,x가 이럴 때 얘가 참이며 int임을 알 수 있고 context에 아무것도 없을 때 2+2가 int임을 항상 알 수 있다

Deriving a judgement

Untitled

B가 bool이고 x가 int일 때 쟤가 int임을 알아야 한다

→ 이를 위해서는 세가지를 알아야 한다 그리고 이 때 b,x는 type context로 미리 알고 있다 -> 세가지를 먼저 보여준다면 이 원하는 구문이 well type인지 알 수 있다

General rule

Untitled

어떠한 type environment a에서 어떠한 expression e가 있고 statement가 있을 때 판단은

T라는 type judgment가 항상 참이려면 세가지 조건이 참이여야 한다

S1,s2 Type이 같아야 한다

Inference Rules

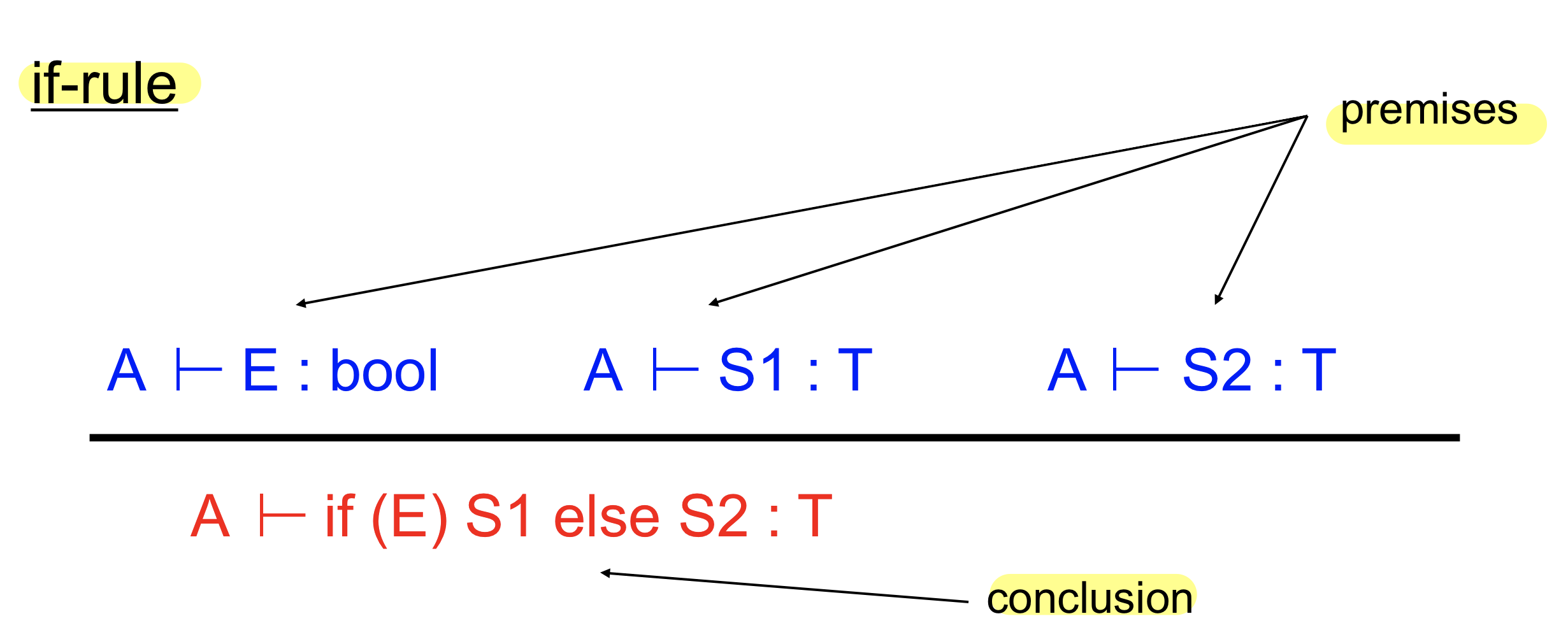
Untitled

추론 룰, 어떠한 세가지가 참일 때 아래의 if 구문이 참이다 이때 결론을 도출하기 위한 세개의 조건을 전제, premises이고 이게 참이면 conclusion이 참임을 알 수 있다

  • 중간 라인 위에 나열된 전제들이 모두 존재하면 아래에 있는 conclusion을 도출할 수 있다
  • Semantic check를 하기 위해 이러한 static semantic의 inference rule을 이용해서 체크하게 된다.

inference rule이 왜 필요한가?

  • Static semantics를 specify하기 위해서 간단하고 정확한 language로
  • Inference rule은 ast를 traversal하면 바로 나오기에(symbol table에서 데이터를 넣어놓고 구문을 맞출 때 마다 ast를 traversal하면 똑같은 순서로 나오게 되어 추론이 가능)
  • Type checking은 inference rule을 거꾸로 들어가면서 문제가 없음을 알아보는 것

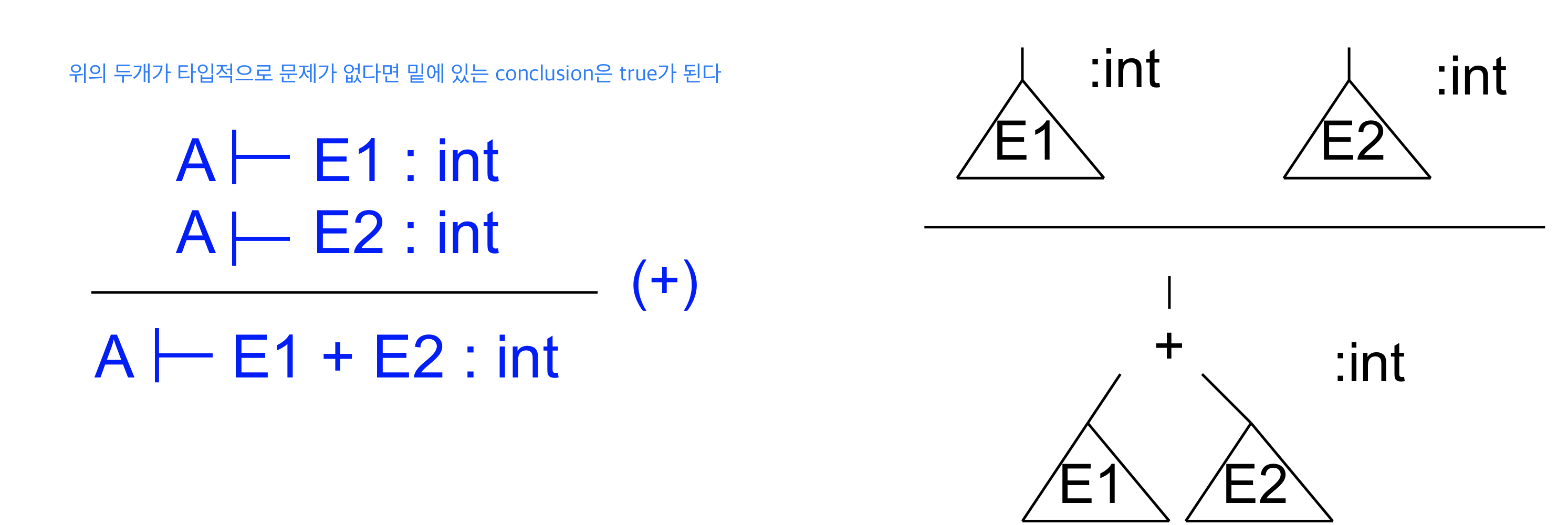
Meaning of inference rule

Inference rule은 먼저 가지고 있는 전제들이 참일 때 conclusion도 참이다

위의 두개가 타입적으로 문제가 없다면 밑에 있는 conclusion은 true가 된다

Untitled

Proof Tree

  • Type judgement가 참인지 아닌지 알기 위해서 inference rule을 거꾸로 찾아가고 이것을 proof tree라고 한다
  • 어떠한 구문은 type judgement를 derive할 수 있을 때 well typed라고 한다
  • type derive해주는 과정을 proof tree이라고 한다

Untitled

만약 a1이라는 context에서 b는 bool이고 x는 int라는 context를 갖고 있을 때 결국 원하는 마지막 수식을 만들 수 있음 -> int이므로 type judgement가 참이 된다

More about inference rule

  • Symbol table에 값이 없더라도 지정해주지 않아도 원래 정해져있는 것들 : axiom

Untitled

  • Judgement는 true임이 증명되는 것은 여러가지 경우로 증명이 가능

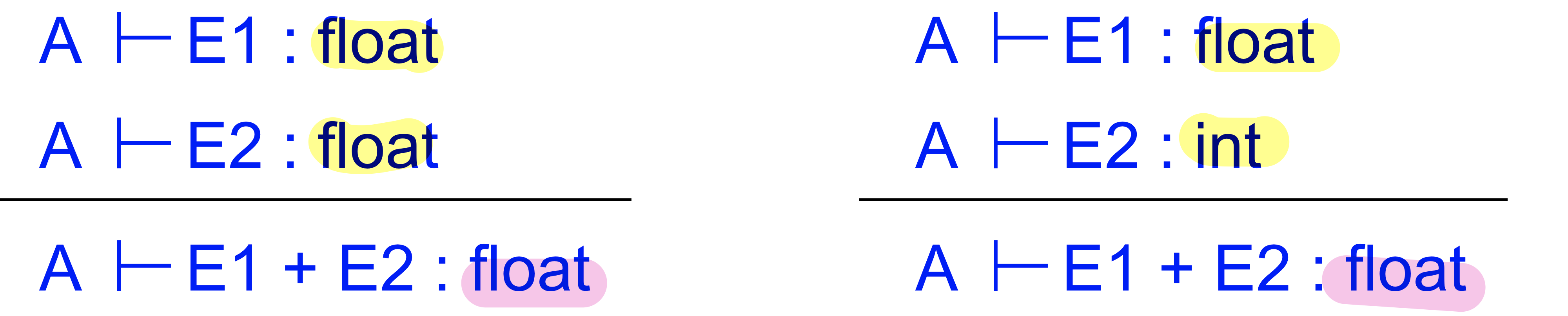
Untitled

이런 것들은 언어마다 다름. 허용할수도 안허용할수도 language가 inference rule을 융통성있게 하느냐에 따라서 judgement가 엄격하거나 유연성을 가질 수 있음

Assignment statements

Untitled

어떠한 variable id이 context에 있고 이게 t type으로 정의되어있음.(symbol table에 id가 있음을 의미)expression이 t일 때 그걸 e에 저장한다면 t 으로 well type이라고 볼 수 있다

Untitled

Array assign도 e1은 t의 배열이고 e2는 int니까 인덱스가 되고 t type으로 잘 지정이 된다

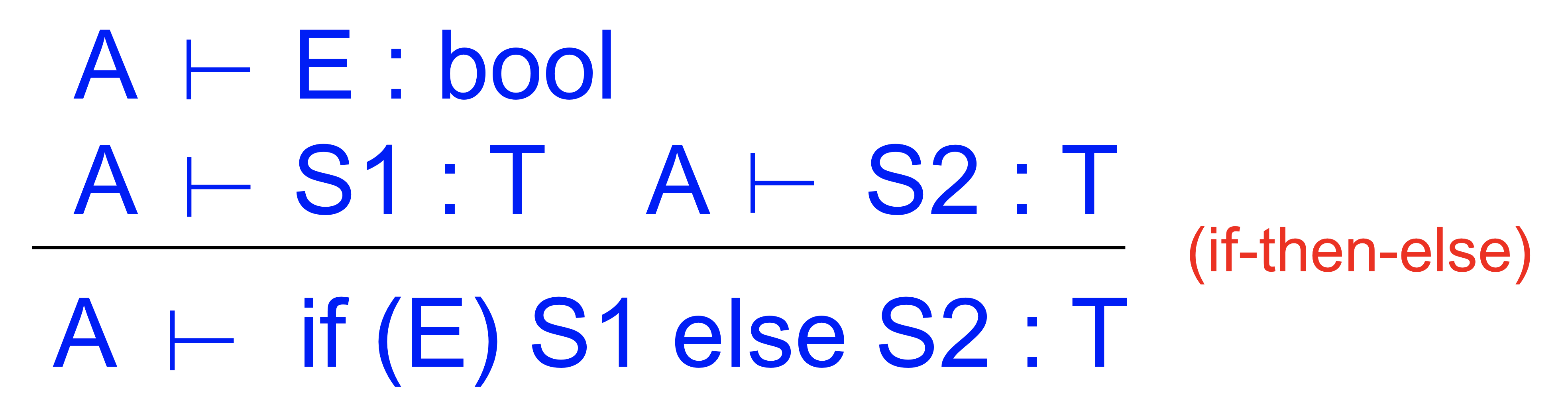
if statements

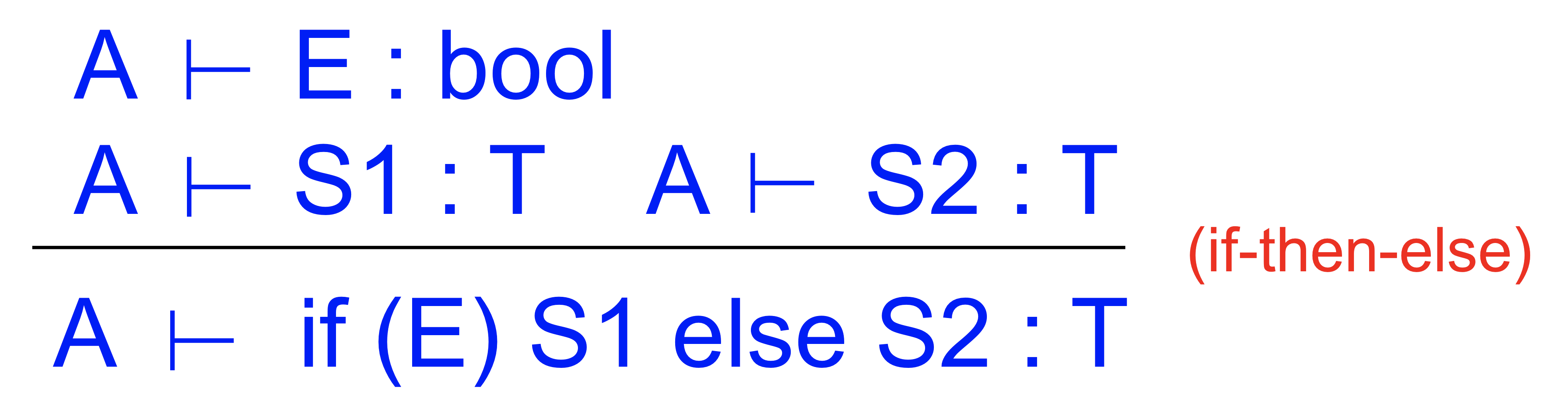
Untitled

근데 여기서 최종타입이 s이거나 아무것도 안되기 때문에 Unit type임

Untitled

Sequence Statements

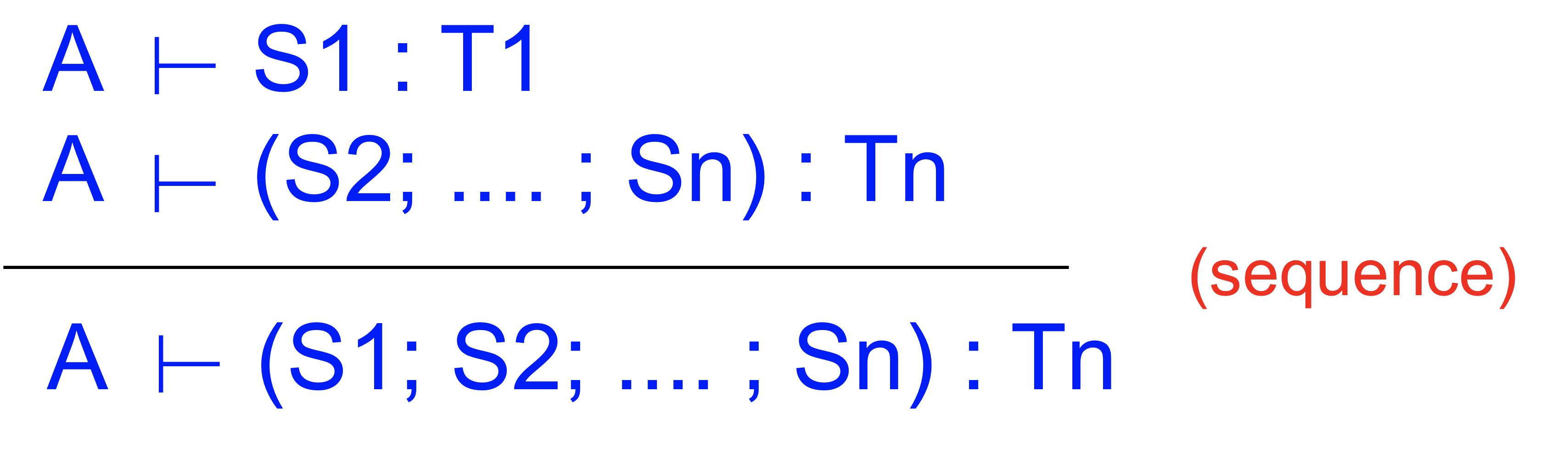
Untitled

Statement가 많을 경우 이 sequence가 well type가 되려면 처음부터 끝까지 모든 statement가 well type일 때 sequence가 well type이 된다

Declarations

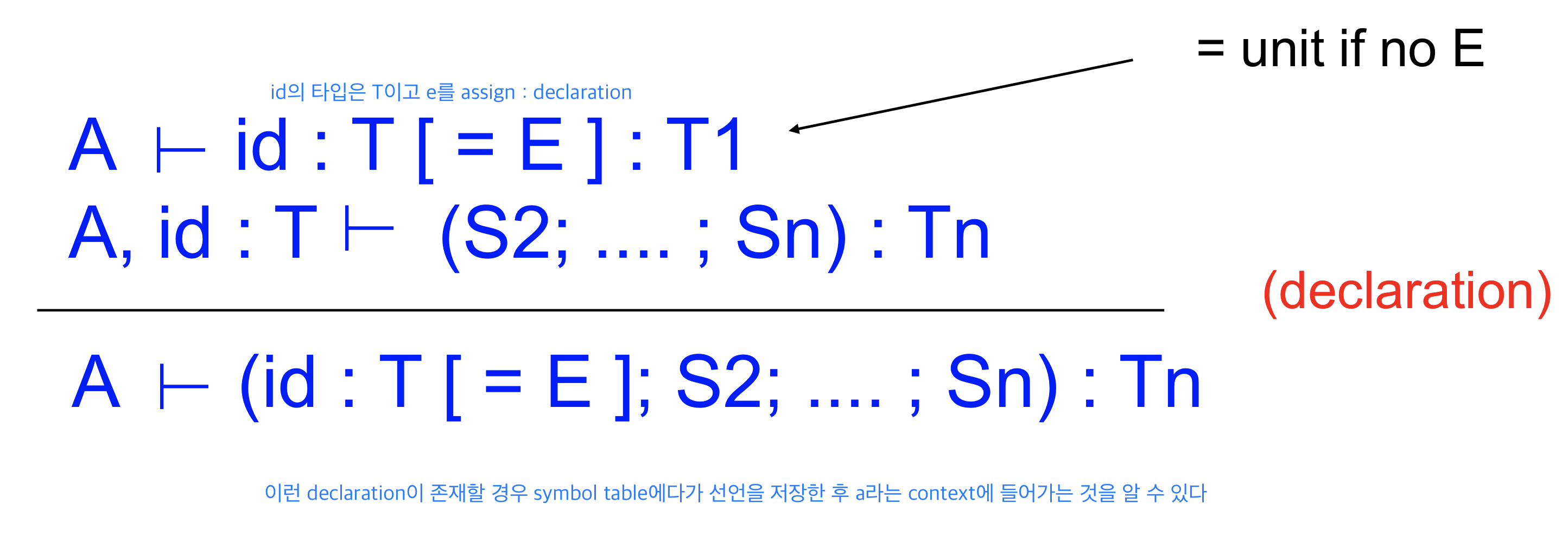
Untitled

이런 declaration이 존재할 경우 symbol table에다가 선언을 저장한 후 a라는 context에 들어가는 것을 알 수 있다

Functions Calls

Untitled

만약 function call이 있다면 모든 argument와 return value의 타입이 모두 잘 맞아야 한다

  • Function call과 어딘가에 선언된 function의 타입이 맞아야 한다(t1…tn(argument 타입)이 맞아야하고 리턴타입까지 맞아야하고 매개변수 개수도 맞아야하고 return이 하나있어야한다)
  • 각각의 t type들이 맞아야 한다-> 그럴 경우 function type이 well typed

Function의 structure가 맞아야하고 function type은 argument 개수, return value 하나있는 것이고 각각의 argument, return value의 타입이 맞아야 한다

Function Declarations

Function이 있다면 리턴타입이 맞아야하므로 리턴타입을 symbol table에 집어넣어주는 것이 중요

  • function 선언시 argument타입이 다 맞고 return expression이 type이 맞아야 well typed이다

→ Function type을 environment에 넣어주는 것이 중요

Mutual Recursion

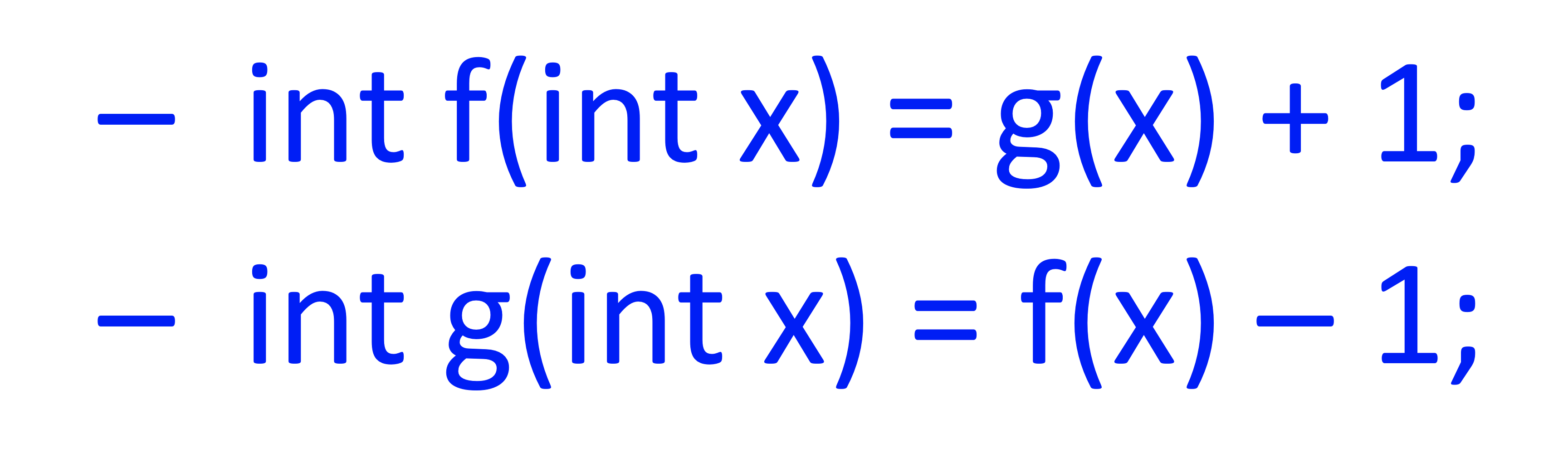
Untitled

어떠한 f,g함수가 있다면 각각 서로의 함수로 만들어지는 경우 f의 정보 g의 정보가 environment에 모두 들어가 있어야하는데 어떤 순서가 되든 두 개 중에 선언이 되어있지 않으므로 타입 checking에 문제가 됨 -> two pass approach가 된다

먼저 ast를 다 만든 뒤 global environment를 만드 후 type checking을 하면된다

How to Check Return?

Untitled

결국 output이 없으므로 unit type이긴 하지만 expression이 타입을 가지고 있을 때 비교할 타입이  없음

이 타입이 맞는지 판단 불가 -> return instruction을 수행하는 function에 의존

따라서 return value는 function call시 정해지기에 그 타입을 symbol table을 저장해주면 return. Type을 체크할 수 있음

Untitled

리턴타입을 function call 시 symbol table에 넣어주면 리턴 시 제대로 체크 가능

어떤 function의 리턴타입이 t임을 a에서 알게 되고 return e가 well type되는지 e와 return type을 봐서 판단 가능

(static semantic 정리)

Static semantic은 type checking을 spec으로 저장할 수 있는 방법이며 static semantic을 간결하게 표현 가능 수식이나 구문은 inference rule로 proof tree를 만들 수 있다면 well type임을 알 수 있고 만들 수 없다면 type errorr가 있는 수식임을 알 수 있다

(semantic analysis 정리)

Lex,syn으로 detect할 수 없는 에러를 찾는 것이고 크게 찾는 것이 scope 에러와 type 에러가 존재 scope은 variable이 그 scope에서 define되지 않았다거나 여러개가 선언될 경우 문제 type error를 열심히 마치게 됨

프론트 앤드가 끝나고 IR을 만든 뒤 백엔드로 가는데 다음에는 ast에서 IR을 만드는 법에 대해서 알아보자!