- 이제는 data flow analysis를 끝냈기 때문에 실제로 코드를 최적화하는 기법들에 대해서 알아보자
기본적으로 타겟 프로세서 해당 코드를 빠르게 구동시키는데 집중하고 있음 속도가 최선의 목표이기 때문, 하지만 iot 디바이스의 경우 실제로 원하는 타겟 스피드를 맞추면서 최소한의 비용으로 시스템을 꾸리기 원하기 때문에 코드 사이즈가 작는 것이 중요함. 메모리에 들어가는 비용을 줄일 수 있기 때문에 파워와 코드사이즈가 더 중요. 슈퍼 컴퓨터의 경우에는 속도가 빠른 게 매우 중요
물리 현상을 수행하는 슈퍼컴퓨터는 3일 걸리던 작업이 1.5일에 걸린다면 결과를 보는데 매우 중요함
머신러닝 어플리케이션도 핵심 어플리케이션이 되었는데 계산량도 매우 많기 때문에 속도를 빠른 것이 최선
Optimization의 중요
Code optimization
- make the code run faster on the target processor(+power, code size)
classes of optimization
- Classical(machine independent) : 머신과 상관없는 최적화
-
instruction 수를 줄이는데 집중, redundancy elimination이 핵심, 중복된 코드를 삭제
Ex) c로 짠 언어를 머신 코드로 바꿔주면 중복코드가 많음.
R1= r2+r3 ;..
R1= r2+r3; 이러면 하나를 지워줄 수 있음
이런 코드가 많은 편이며 컴파일러가 알아서 최적화를 잘 해줌
-
operation을 simplify(strength reduction, instruction 강도를 줄인다. 오래 걸리는 연산을 짧게 거리도록 한다)
그 다음 어떠한 작업을 심플하게 바꿔주는 작업도 수행 : 곱하기를 쉬프트로 바뀌도록 하던가
-
모든 machine에 적용 가능
이러한 최적화들은 어떤 머신이더라도 대부분 다 적용이 되는 최적화임. 연산량을 줄이고 헤비한 연산을 light한 연산으로 바꿔주는 것이기 떄문에 근본적인 것을 바꿔주기 떄문에 대부분의 머신에서 수행 가능
-
- machine specific
- peephole optimization
- take advantage of specialized hardware features
이런것들은 타겟하드웨어의 특성을 알아야 한다
-어떤 프로세서는 브랜치의 오버헤드가 엄청커서 브랜치의 오버헤드를 줄여야 함-> 브랜치 instruction을 줄여주는 최적화를 수행할 것
-어떤 프로세서는 브랜치 오버헤드가 많지 않기 때문에 효율적인 코드, 브랜치에 상관없이 만들어도 상관없음
Ex)Function inlining은 function call시 call instruction을 통해서 수행되게 하는데 function을 그냥 caller의 코드로 변환해서 카피해버리면 call instruction이 필요없음. 브랜치나 call instruction의 오버헤드가 큰 경우 function inlining을 많이 수행하는 것이 좋음. Function call, branch 오버헤드가 크지 않으면 열심히 수행할 필요 없음
- 여러개의 instruction을 한번에 여러개 수행할 수 있는 병렬 연산 유닛이 들어간 경우가 있고 이걸 잘 사용할 수 있는 코드를 만들어주는 target hardware specifc한 최적화도 존재
- 병렬화(Parallelism enhancing)
- increasing parallelism(ILP or TLP)
-
대부분의 프로세서는 한사이클에 여러 instruction을 수행할 수 있음. 가능하다면 한사이클에 최대한 instruction을 많이 수행할 수 있도록 dependency를 없애줘야 한다. 이러한 최적화를 수행-> 병렬성을 높임
Cpu가 여러개 있는 멀티 코어의 경우 멀티쓰레드로 돌릴 수 있으니까 하나의 프로그램을 멀티 쓰레드로 자동으로 바꿔주는 최적화도 생각할 수 있음
-
- possibly increase instructions
→ 여기서는 classical에 대해서만 알아볼 것, 이름이 직관적인 편이며 방법도 직관적, 그래프에서 어느 부분을 지우거나 순서를 바꾸거나 그래프마다 time을 지정(스케줄링) 등의 graph processing이라고 볼 수 있음.
A Tour Through the classical optimizations
- 중요한 거는 많은 최적화 중에서 몇개를 볼 것인데 컨셉을 볼 것인데 완벽하게 아는 것보다는 이 최적화가 무엇을 하는 것이며 왜 효과적인가, 최적화는 언제 적용될 수 있는지, 실제로 어떻게 동작하는지에 대해서 알면 좋을 것
- 최적화 중에서 여러가지 생각할 것들이 존재 :
-
register pressure을 생각해야함. 코드를 최적화하기 위해서 코드를 변경했는데 레지스터를 너무 많이 쓰는 최적화가 되는 경우가 될 수도 있음.
Ex) ARM 프로세서는 16개의 레지스터가 있는데 a,b,c 변수가 세개가 있다면 dependency를 없애기 위해서 ssa form으로 바꾸면 a(0,1,2..)b(0,1,2…)c(0,1,2,3..)으로 변수의 개수가 엄청 많아져서 변수마다 레지스터를 할당하면 16개를 넘어서 암에 모두 다 저장할 수 없게 됨 -> 메모리에 일부를 저장해야하기 때문에 메모리에 변수를 가져올 떄 마다 딜레이가 길어질 수 있으므로 항상 지금 살아있는 레지스터 수가 항상 작은 것이 중요
-
parallelism verses operation count : 병렬화를 하면 instruction의 수가 늘어나기 때문에 그것에 대해서도 생각해야 함
-
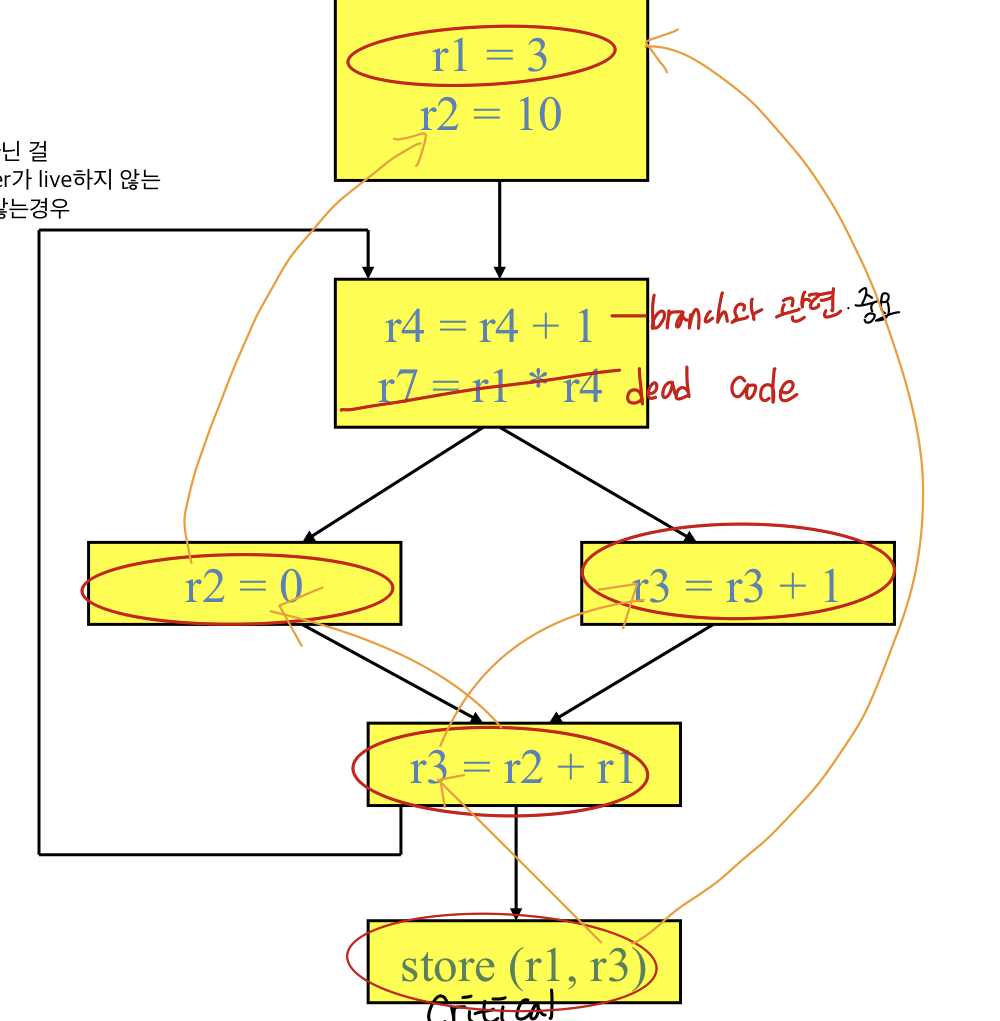
Dead Code Elimination
기본적으로 instruction이 절대 그 결과가 끝까지 사용되지 않는 instruction이 존재, 이건 실행할 필요가 없음. 나중에 사용하지 않으므로!
- 의미 : result가 사용되지 않는 operation 삭제
Dead code : store와 상관되지 않는 명령어가 dead code임. 메모리에서 데이터를 읽어와서 데이터를 바꾸고 메모리에 다시 쓰는데 디램에 쓰고 끝나면 안됨. 스토리지에 저장되어야 끝나는데 데이터를 디램에 적으면 무조건 스토리지에 들어간다고 무조건 가정하고 있으니까 메모리에 데이터를 쓰면 스토어 instruction이 있다면 스토어와 관련된 코드들은 다 필요한 것이라고 볼 수 있음-> store와 연결되지 않는 코드를 없애야 한다
Ex)
R4= r1+r5 -> 삭제
R3 = r1+r2
- r4는 저장되지 않으므로 없애도 된다.
Q. Instruction이 많이 있는데 store와 관련있는지 어떻게 알까?
A. Data-flow analysis를 통해서! Def-user가 있음(DU chain)
sw(r3)
R3= r1+r2
Sw(r3) : r3를 use, 어디선가 r3가 만들어지고 r3의 def임
→ Du chain으로 instruction을 찾을 수 있음 store부터 시작해서 definition을 사용하고 r1,r2를 use니까 r1,r2를 찾아서 관련된 Instruction을 du chain으로 위로 올라가면서 찾고 그 chain과 연결되지 않는 코드를 지워주면 된다.
⇒ 결과가 끝까지 사용되지 않는 instruction을 지우는 것
- Rules
- store, branch가 아닌 operation x는 지울 수 있다(store, conditional code는 무조건 살아야 하고 나머지가 dead code가 된다)
- DU chain이 empty나 dest register가 살아있지 않다면
- Du chain이 사용되지 않거나 dest register가 live하지 않는 (어딘가 사용), def는 되었는데 사용하지 않는경우 live하지 않다면 지울 수 있다
- Dead code를 찾기 위해서 어떻게 찾는가?
-
Critical operation(store or branch operation)을 찾음. 무조건 수행해야 하기 때문에 중요
critical operation에 데이터를 제공하는 instruction
- directly or indirectly feed a critical operaiton하지 않는 것은 dead
- Directly는 du chain이고 indirect는 multiple du chain임
- Store와 연결되지않는게 dead code
- 값을 만드는 def는 Producer/ 값을 이용하는 use가 consumer
- store을 찾아서 store을 만드는 instruction을 만드는 instruction을 체크하면서 체크되지 않은 코드를 지우면 된다.
-
critical chain부터 ud chain 거꾸로 가면서 trace
Ud chain은 use로 def를 찾는 것, store부터 가서 관련된 체인을 ud chain으로 찾고 한번도 찾지 않는 것은 지워도 됨
-
local constant propagation
Local : 하나의 intra bb <-> global : inter bb
→ 글로벌은 여러개의 bb에서 전체적으로 보는 것이고 로컬은 하나의 bb에서 보는 것
Constant propagation : 상수를 전달한다
-
forward propgation of moves of the form
하나의 블럭 안에서 어떠한 레지스터가 (constant)인 경우 어디까지 전달되는지 보고 얘를 constant로 바꿀 수 있음
- rx = L(L은 literal)
- maximally propagate

두개의 Operation이 있고 x,y가 있는데 x가 y보다 먼저 실행될 때 x: rx = L이고 x의 source가 상수라면 (이게 아니라면 r1=r2도 있는데 얘는 constant가 아님) y라는 Instruciton x의 소스를 사용하는 경우(y=ra=rb+rx) 그리고 이 사이에 rx가 다시 정의되지 않는다면 xy사이에 x를 없애버릴 수 있음
- Constant를 이용한 먼가가 있고 얘를 무브의 destination 값을 input으로 사용하는 애를 찾아야 하고 그 사이에 레지스터가 다시 정의되면 안된다는 조건을 찾아야 함.
- X,y가 하나의 bb 안에 있는데 x가 무브인데 x의 source는 상수이고 y는 x의 dest를 Use한다. 그리고 이 사이에 dest x의 새로운 정의가 있으면 안됨. 5번은 사실 별로 안중요함. 알 수 없는 먼가가 있으면 안된다는 의미로 컴파일러는 무조건 문제가 없는 최적화만 수행하기 때문에 macro, function all은 나의 스콥에서 안보이기 때문에 안전하게 하기 위해 최적화를 안함
- Instruction 수가 줄고 레지스터 operand가 없어져서 Register pressure가 줄 수 있음

R1 =5에서 5는 상수인데 r1을 사용하는 데를 찾아서 상수로 바꾸면 무브를 없앨 수 있다. 또한 여분의 레지스터가 생김 Cpu,gpu에서 아주 중요한 자원이 레지스터인데 r1에 5에 저장하는 걸로 너무 오래 저장하는데 constant propagation을 통해서 그 레지스터로 다른 값을 저장할 수 있게 되므로 더 중요한 것
Q. 밑에 있는 r1은 왜 업데이트가 안될까?? 이거 매우 중요 : 새로운 definition이 생기기 때문, 5가 아니기 때문, 새로운 r1이 생겨서 다른 것이기 때문에 잘 체크해야 함
R4가 다른 걸로 변하게 되면 r4=r4+5 없어질 수 있다
global constant propagation
local constant propgation과 동일하며 글로벌인 것만 다름, Inter bb를 의미
여러개의 블럭 사이에서 어떠한 레지스터가 (constant)인 경우 어디까지 전달되는지 보고 얘를 constant로 바꿀 수 있음

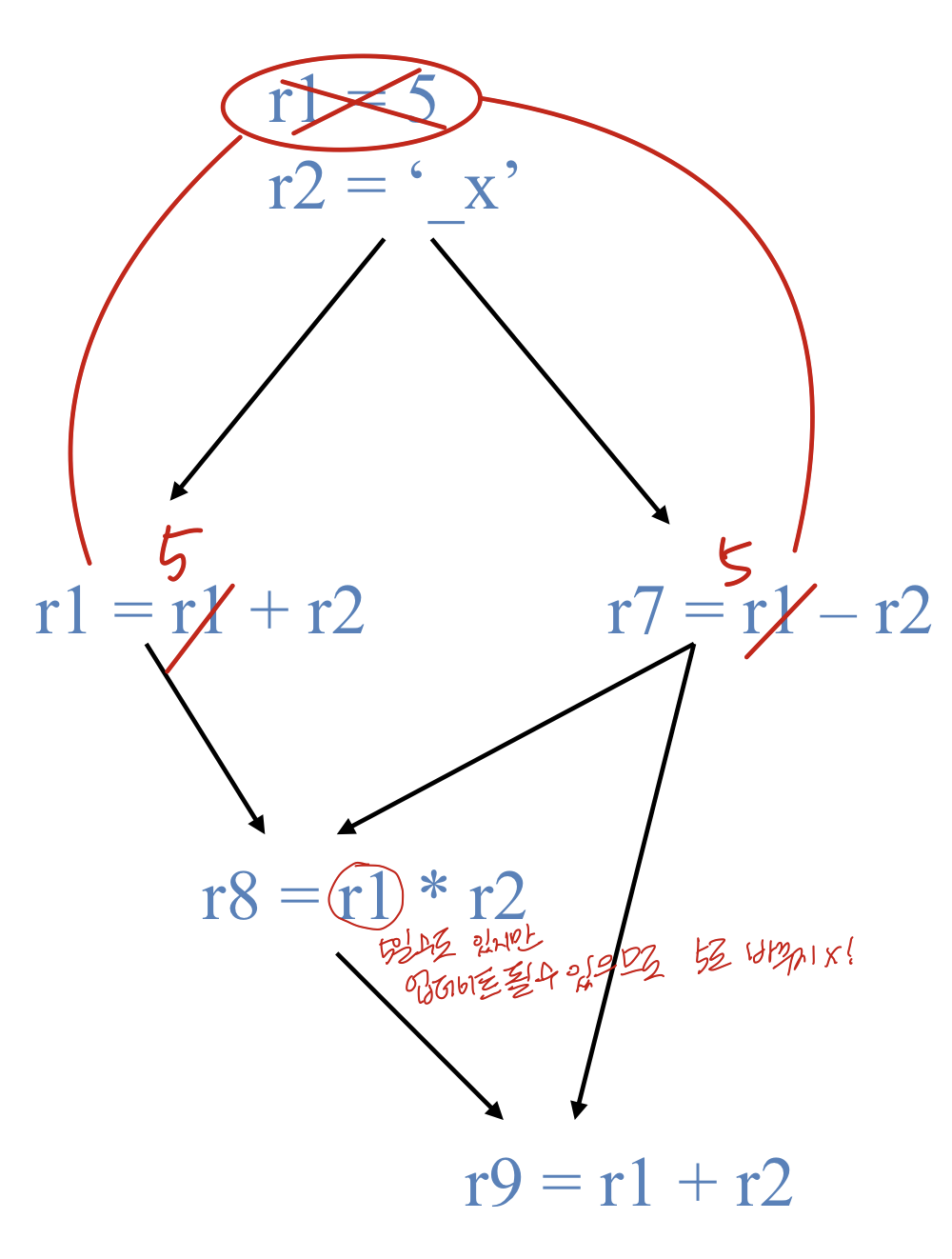
r8안되는 이유 알기
✅Constant Folding
상수를 돌돌 만다. 어떠한 operation이 있을 때 하나의 오퍼레이션을 심플하게 바꾼다, 중요한 기법
- simplify 1 operation based on values of src opearnds
ex) R1 = 3*4 -> 12로 변경, 곱셈을 한번만 하게 되므로 곱셈이 줄어 strength reduction이라고도 부른다.
모두 constant operand인 경우, 수학적으로 동일한 경우 같은 연산을 변경
Q. 이런 경우가 실제로 있는가?
A. Constant propagation와 다른 최적화를 수행한다면 그 결과로 constant folding을 할 수 있는 경우가 많아짐, 프로그래머가 비효율적으로 짜기 보다는 최적화를 하다보니 생기는 것
R2=r3
R3=4
R1=r2 * r3
- R1 = 3*4로 바뀌는데 이때 constant folding이 가능
→ Constant propagation하면 생길 가능성이 커짐
-
0과 관련된 것 1과 관련된 것도 존재
