Pattern matching

밑에처럼 선언하게 하면 좀 더 수학적인 정의에 가깝게 선언 가능하기에 좋다!

Fibonacci Series

문제는 너무 느림

→ 어떻게 빠르게 만들 수 있을까? 결과를 기억하도록 하면 원래는 매번 recursion을 두번하던 거를 한번만 해도 된다!!!

fun fibo 0 = (1,1)
| fibo n = 
let val (n_1,n_2) = fibo(n-1)
in
	(n_1+n_2, n_1)
end

• memorization하자: side effect없는 function(don’t have state)이면 cash해서 해보쟈!
• 속도 vs more memory space: trade off

→ 키가 argument, 벨류가 리턴값으로 캐싱해야함

→ recursion을 한번만 하게 되어서 속도가 올라감~

Nested patterns

pattern 안에 pattern이 있을 수 있음

• 패턴은 값을 매칭하고 추출하기 위한 일반적인 개념인 반면, 중첩 패턴은 중첩된 데이터 구조에서 값을 매칭하고 추출하기 위한 특정 유형의 패턴
• matching whole thing and each part of sub pattern이 맞는지 봄
• pattern matching의 정의
  • 패턴을 same shape에 대한 값과 비교하고 변수를 right part에 바인딩하는 것을 의미

ex) zip3 & unzip3 - nested pattern 맞음

(*
([1,2,3],[10,20,30], [100,200,300]) => [(1,10,100),(2,20,200),(3,30,300)]
*)
exception myException;
fun zip3 lists =
case lists of
([],[],[]) => []
|(hd1::tl1,hd2::tl2,hd3::tl3) => (hd1,hd2,hd3)::zip3(tl1,tl2,tl3)
|_ => raise myException;

zip3([1,2,3],[10,20,30], [100,200,300]);

(*
[(1,10,100),(2,20,200),(3,30,300)]=> ([1,2,3],[10,20,30], [100,200,300])
*)
fun unzip3 triples =
case triples of
[] => ([],[],[])
|(a,b,c)::tl => 
	let val (l1,l2,l3) = unzip3(tl)
	in (a::l1,b::l2,c::l3)
	end;

unzip3 [(1, 10, 100), (2, 20, 200), (3, 30, 300)];

ex) Nondecreasing- nested pattern은 아님

(*배열이 점점 느는 형태인지 체크하는 함수*)
fun nondcreasing xs = 
case xs of
[] => true
  | x:: [] => true
  | x1::x2::_ => x1 <= x2 andalso **nondcreasing (tl xs);**

ex)multsign

datatype sgn = P|N|Z;
fun multsign(x1,x2)=
let fun sign(x) = if x>0 then P 
            else if x<0 then N 
             else Z
in
  case (sign(x1),sign(x2)) of
  (P,P) => P
  |(N,N) => P
  |(P,N) => N
  |(N,P) => N
  |(_,Z) => Z
  |(Z,_) => Z
end;

datatype sgn = P|N|Z;
fun multsign(x1,x2)=
let fun sign(x) = if x>0 then P 
            else if x<0 then N 
             else Z
in
  case (sign(x1),sign(x2)) of
  (Z,_) => Z
  |(_,Z) => Z
  |(P,P) => P
  |(N,N) => P
  |_ => N (*이게 낫대*)
end;

ex) card_sml

is_flush: 손에 있는 카드가 같은 shape인 경우 flush됨. 손에 든 카드가 모드 같은지 체크하는 함수

• 손에 아무것도 없을 때나 하나만 들고 있을 때에는 상관없이 true,
• 두개 이상의 카드가 있는 경우: 같은 shape이라면 true

fun is_flush(hand: card list): bool =
case hand of
[] => true
|Card(_,_)::[] => true
|Card(s1,_)::Card(s2,_)::_ =>
s1 = s2 and also is_flush(tl hand);

is_straight: 손에 있는 카드가 숫자가 인접한지 체크하는 함수

• 일단은 주어진 list를 sort해야 함
• special case ace card: 10,j,q,a도 맞고 ace,1,2,3,4도 되고…? 카드게임 모르는뎅

	fun is_straight(hand: card list): bool = (*우리보고 해보래*)
  case hand of
  [] => true
  |Card(_,_)::[] => true
  |Card(_,Num(10))::Card(_,Jack)::_ => is_straight(tl hand)
  |Card(_,Jack)::Card(_,Queen)::_ => is_straight(tl hand)
  |Card(_,Queen)::Card(_,King)::_=> is_straight(tl hand)
  |Card(_,King)::Card(_,Ace)::_=> is_straight(tl hand)
  |Card(_,Aces)::Card(_,Num(2))::_=> is_straight(tl hand)
  |Card(_,Num(i))::Card(_,Num(j))::_ => if i+1=j then is_straight(tl hand) else false
  |_=> false;

• blackjack: 모든 카드의 숫자를 더한 후 21이 되면 되고 21보다 작으면 점수가 되고 넘으면 지는 거
  • 잭퀸킹은 10으로 하고 ace는 1이나 11 중에서 큰 거 고를 것
  • 살짝 틀리게 했대. 코드 보래

      
    fun blackjack(hand: card list) = 
    let val sum = simpleSum(hand)
    		fun simpleSum(hand: card list) =
        case hand of 
              Card (_, Ace)::rest => 11 + simpleSum(rest)
            | Card (_, Num(i))::rest => i + simpleSum(rest)
            | Card (_, _)::rest => 10 + simpleSum(rest)
            | _ => 0;
    in
        if sum < 21
        then sum
        else if sum > 21 andalso hasAce(hand)
             then 1+blackjack(removeFirstAce hand)
             else sum
    end;
  

Style

• nested pattern은 쉽게 pattern을 표시하고 간단한 코드를 쓸 수 있게 해줌
  • nested pattern이 좀 더 쉽다면 nested case expression은 쓰지 말 것
  • avoid necessary branch나 let expression을 피할 것
  • ex) unzip3, nondecreasing
• tuple을 매칭한 후에 비교
  • ex) zip3,multsign
• wildcard를 사용한다면 필요없는 데이터의 변수를 대신할 수 있어 data binding을 막아줌
  • ex) len, multsign

fun len(l: 'a list) =
case l of
	[] => 0
	|_::l' => 1+ len(l');

Most of the full definition

patternmatching은 pattern p와 value v를 받아 1.match한다면 2.varaible binding을 진행

ex)

a::b::c::d ⇒ 3개 이상의 요소를 가진 리스트면 매치됨

a::b::c::[] ⇒ 3개의 요소를 가진 리스트면 매치됨

((a,b),(c,d))::e ⇒ non-empty list of pair of pair면 매치됨

Exception

• exception binding은 a new kind of expression을 소개
  • define own exception
  • datatype definition과 매우 비슷

exception MyFirstException
excpetion MySecondException of int * int

• raise primitive로 excpetion을 throw

raise MyFirstException
raise (MySecondException(3,4))

• handle expression로 excpetion을 처리할 수 있음
  • handle 은 패턴 매칭과 매우 비슷한 편
  • 매치되는 exception이 없다면 exception은 계속 전파됨
  • 이 때 e1,e2,e3의 타입은 동일해야 함

e1 handle MyFirstException => e2
					| MySecondException(x,y) => e3

exception InvalidArgument;

fun max2(xs: int list) =
 case xs of
[] => raise InvalidArgument
| x::[] => x
| x::xs' => Int.max(x, max2(xs'));

max2([]);
max2([]) handle InvalidArgument => 0;
max2([]) handle InvalidArgument => "hi"; 
// 에러. 함수의 리턴타입과 handle의 타입이 안맞아서

• Int.max를 쓰게 되면 라이브러리를 쓰는 건데 그러면 라이브러리가 로드됨
• 중간에서 exception이 일어난다면 코드가 중간에서 멈출 것

fun max3(xs: int list, exc) = 
 case xs of
[] => raise exc
| x::[] => x
| x::xs' => Int.max(x, max2(xs'));

max3([], MyCustomExc) handle InvalidArgument => 42 
														| MyCustomExc => ~200;

• 사용하는 함수는 context를 알기 때문에 0을 리턴해도 됨. callee는 모르니까 0을 쓰는게 안좋은 거임
• exception을 파라미터로도 보낼 수 있음

→ warning을 주지 않아 좋은 점

• 패턴매칭은 모두 다 리스팅을 해야하지만 exception은 리스팅을 하지 않아도 됨. 자바에서는 function call이 중첩 많이 되어있는데 innermost한 애가 exception났다면 어느 레벨에서 처리할건지는 프로그래머가 처리하는 게 맞는데 자바에서는 throw를 다 적어야 함.
• throw가 진짜로 되어야 하면 handle이 필요없는 경우도 있어서 모든 경우를 처리하지 않아도 에러가 나지 않는 거이기도 함

Recursion

• recursion은 loop을 사용하는 것보다 쉬움
  • ex) tree, appendling list
  • divide and conquer 방식

Call - stacks(== activation record, function frame)

• 프로그램이 실행될 때 시작했지만 return되지 않은 function call 시 call stack이 존재
  • function f를 호출 시 f의 인스턴스가 스택에 추가
  • f가 끝날 때 pop stack됨
• stack-frame에 있는 내용
  • local variable과 함수에 아직 해야할 일이 저장됨
  • ex) local variable, position 등등…

→ recursion하게 되면 call stack에 동일한 함수들이 쌓이게 됨

function frame이 recursive보다는 loop으로 하는 게 좀 더 덜 expensive함. 메모리나 calling overhead때문

cf. cpython eval함수 안에 while loop 존재, 실제 함수는 힙에 존재 스택에는 eval함수만 존재

→ 더 expensive니까 cheap하게 해보쟈!: tail recursive version

ex) recursion → tail recursion

• recursive 함수가 동일하게 있지만 이전꺼는 리턴한 후에 계산을 해줬어야 하는데 지금은 리턴만 하면 되니까 좀 더 가벼워짐
  • 즉, recursive call의 결과가 caller의 결과가 된다!

An Optimization

• tail recursive을 통해 callee의 결과를 받아서 더이상 계산안하고 return하면 되기 떄문에 stack frame을 전부 유지할 필요가 없게 됨!!
• ML은 tail call을 인지해서 컴파일러는 아래처럼 작동
  • call하기 전에 pop the caller한 후 callee은 reuse the same statck space하도록 함
  • tail code를 컴파일러를 보게 되면 recursive를 루프로 자동 바꾸게 해줌

→ reuse stack frame

Non Tail → Tail recursion

1. helper function 생성: 원래 똑같은 모양이지만 accumulator를 추가로 받음
2. old base case(helper최초호출 시)는 accumulator의 초기값으로 변경
3. new base case(helper안)는 final accumulator로 변경!

fun sum xs =
case xs of
[] => 0
  |x::xs' => x+ sum(xs')

fun sum2 xs = 
let fun aux (xs, acc) = 
  case xs of
  [] => acc
  |x::xs' =>  aux(xs', acc +x) (*keep tempary result, foo(aux..)이면 tail position이 아님*)
in
  aux(xs,0)
end;

fun rev xs =
  case xs of
  [] => []
  |x::xs' => rev(xs') @ [x]

(*
xs = [1,2,3] acc = []
1::[2,3] -> 1::[]
2::[3] -> 2::[1]
3::[] -> 3::[2,1]

*)
fun rev2 xs =
let fun aux(xs, acc) =
  case xs of
  [] => acc
  |x::xs' => aux(xs',x::acc)
in aux(xs,[])
end;

• fact, sum은 tail recursive와 recursive 모두 linear 시간에 종료
• 하지만 rev의 경우 non-tail recursive는 quadratic에 끝남. 왜냐면 @로 인해 리스트를 매번 순회해야 하기 때문에 length*length/2 가 되기에 tail이 훨씬 좋음

cf. c++안에는 비슷한 nested function이 있고 non tail , tail recursive도 존재. 하지만 람다함수는 노말함수보다 좀 더 expensive하기 때문에 밖에 helper function을 선언해서 tail recursive로 바꾸는 게 좋을 것

Always tail-recursive?

• recursive function 중에서 constant amount of space에 evlauate되지 못하는 경우 존재
  • ex) tree 문제, quick sort, binary search tree

  → 이런 거는 natural recursive approach로 해야 함! 바꿔도 의미가 없음

• 따라서 모든 문제를 항상 바꿀 수 있는 게 아님
  • ex) two recursive같은 것은 tail recursive못함

Tail-call

• nothing left for caller to do를 의미
• f x의 결과가 function body의 immediate result가 된다면 tail call이 됨!
• tail call이라면 스택을 쌓지 않고 최적화된 코드를 만들 수 있음, 주로 재귀함수에 존재

tail position

• tail call은 function call in tail position을 의미
• 일반함수에도 존재

cf.

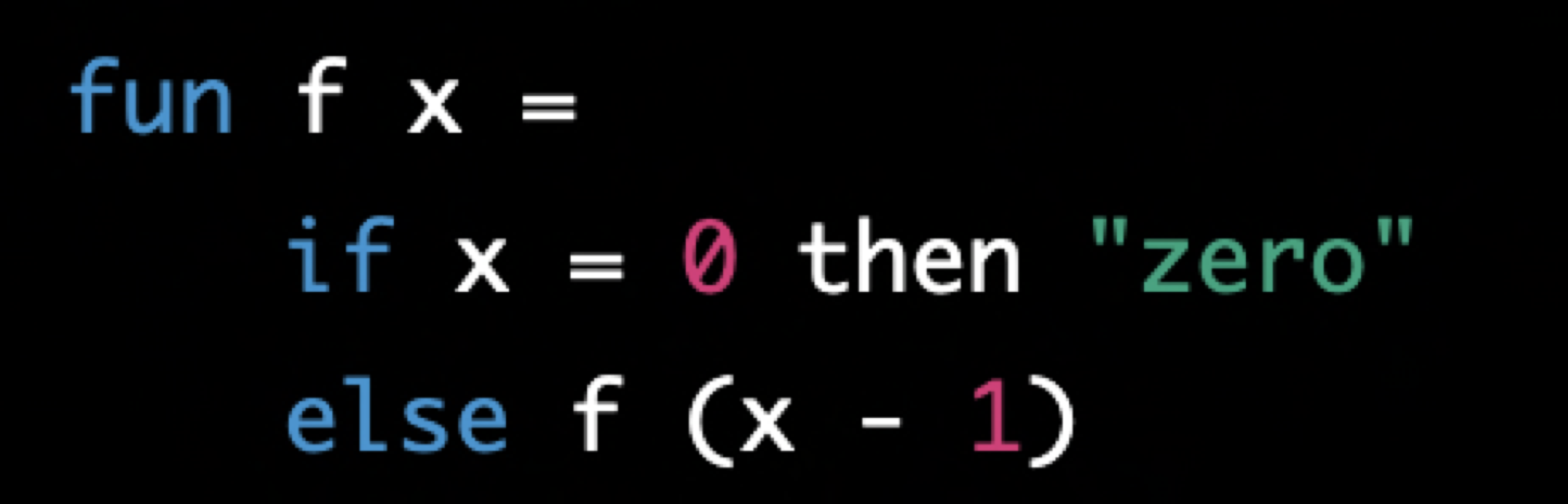
• tail position은 함수가 반환되는 위치를 의미하며, -> 예제 함수 f에서 “zero”와 f (x-1) 모두 함수가 반환하는 위치에 해당하기 때문에 tail position입니다.
• tail call은 함수가 호출하는 위치를 의미합니다. -> 예제 함수 f에서 마지막 문장인 f (x - 1)이 함수 자신을 호출하는 부분이므로, tail call입니다.